Funções de alta ordem
Funções em Haskell podem retornar ou receber outras funções como parâmetros. Uma função que realiza alguma dessas coisas é chamada de função de alta ordem. Funções de alta ordem não são apenas parte integrante do Haskell, mas praticamente o prório Haskell. Quando você quer criar cálculos definindo o que as coisas são ao invés de definir passos que mudam algum estado e talvez fazer uma iteração, funções de alta ordem são indispensáveis. Elas são uma forma muito poderosa de resolver problemas e pensar em programas.
Funções curried
Toda função em Haskell oficialmente recebe apenas um parâmetro. Então, como foi possível quando nós definimos e usamos várias funções que tinham mais de um parâmetro até aqui? Bom, com um truque muito esperto! Todas as funções que aceitaram vários parâmetros até aqui eram funções curried. O que isso significa? Você vai entender melhor com um exemplo. Peguemos nossa boa amiga, a função max. Parece que ela recebe dois parâmetros e retorna o que é maior. Executar max 4 5 cria primeiro uma função que recebe um parâmetro e retorna ou 4 ou este parâmetro, dependendo de qual é o maior. Então, 5 é aplicado à esta função e ela produz o resultado desejado. Isso parece um bocado, e é de fato, um conceito muito interessante. As duas chamadas a seguir são equivalentes:
ghci> max 4 5 5 ghci> (max 4) 5 5
Colocar um espaço entre duas coisa é simplesmente aplicar a função. O espaço é como se um fosse operador e ele tem máxima precedência. Examinemos o tipo de max. Ele é max :: (Ord a) => a -> a -> a. Isso também pode ser escrito como max :: (Ord a) => a -> (a -> a). Isso poderia ser lido assim: max recece um a e retorna (com aquele ->) uma função que recebe um a e retorna um a. É por isso que o tipo do retorno e os parâmetros das funções são simplesmente separados por setas.
Então como isso pode nos beneficiar? Colocando de forma simples, se nós chamamos uma função com parâmetros faltando, recebemos uma função parcialmente aplicada, ou seja, uma função que recebe o número de parâmetros que omitimos. Usar aplicação parcial (chamar uma função faltando parâmetros, se você preferir) é uma maneira de criar funções em tempo real para passá-la a outra função ou alimentá-la com dados.
Dê uma olhada nesta função ridículamente simples:
multThree :: (Num a) => a -> a -> a -> a multThree x y z = x * y * z
O que realmente acontece quando executamos multThree 3 5 9 ou ((multThree 3) 5) 9? Primeiro, 3 é aplicado à multThree, porque eles estão separados por um espaço. Isso cria uma função que recebe um parâmetro e retorna uma função. Então 5 é alocado à esta, que cria uma função que receberá um parâmetro e multiplicá-lo por 15. 9 é passado à esta função e o resultado é 135 ou algo assim. Lembre-se que o tipo desta função também poderia ser escrito como multThree :: (Num a) => a -> (a -> (a -> a)). O negócio antes de -> é o parâmetro que a função recebe e a que vêm depois é o que ela retorna. Sendo assim, nossa função recebe um a e retorna a função do tipo (Num a) => a -> (a -> a). Da mesma forma, esta função recebe um a e retorna uma função do tipo (Num a) => a -> a. E esta função, finalmente, recebe apenas um a e retorna um a. Veja isto:
ghci> let multTwoWithNine = multThree 9 ghci> multTwoWithNine 2 3 54 ghci> let multWithEighteen = multTwoWithNine 2 ghci> multWithEighteen 10 180
Ao chamar funções com parâmetros faltando, por assim dizer, estamos criando funções em tempo real. E se nós quiséssemos criar uma função que recebe um número e o compara com 100? Poderíamos fazer algo assim:
compareWithHundred :: (Num a, Ord a) => a -> Ordering compareWithHundred x = compare 100 x
Se chamamos esta função com 99, ela retorna GT. Barbada. Repare que o x está à direita em ambos os lados da equação. Agora, pensemos sobre o que compare 100 retorna. Ela retorna uma função que recebe um número e o compara com 100. Uau! Não é esta a função que nós queríamos? Podemos escrever isto assim:
compareWithHundred :: (Num a, Ord a) => a -> Ordering compareWithHundred = compare 100
A declaração do tipo permanece idêntica, porque compare 100 retorna uma função. Compare tem o tipo (Ord a) => a -> (a -> Ordering) e chamando-a com 100 retorna um (Num a, Ord a) => a -> Ordering. A restrição de classe adicional aparece sorrateiramente porque 100 também é parte do typeclass Num.
Funções infix também podem ser parcialmente aplicadas usando secções. Para secionar uma função infix, simplesmente coloque ela entre parênteses e passe apenas um parâmetro. Isso cria uma função que recebe um parâmetro e então aplica ele no lado em que está faltando o operando. Uma função absurdamente trivial:
divideByTen :: (Floating a) => a -> a divideByTen = (/10)
Executando, digamos, divideByTen 200 é o equivalente a fazer 200 / 10, bem como (/10) 200. Uma função que verifica se o caracter passado a ela é uma letra maiúscula:
isUpperAlphanum :: Char -> Bool isUpperAlphanum = (`elem` ['A'..'Z'])
A única coisa especial sobre secções é o uso do -. Pela definição de secções, (-4) resultará em uma função que recebe um número e subtrai 4 dele. Entretanto, por conveniência, (-4) significa menos quatro. Logo, se você quer fazer uma função que subtrai 4 de um número que ela recebe como parâmetro, aplique parcialmente a função subtract como neste exemplo: (subtract 4).
O que acontece se nós tentarmos executar multThree 3 4 no GHCI ao invés de associar isto à um nome com um let ou passando à uma outra função?
ghci> multThree 3 4
<interactive>:1:0:
No instance for (Show (t -> t))
arising from a use of `print' at <interactive>:1:0-12
Possible fix: add an instance declaration for (Show (t -> t))
In the expression: print it
In a 'do' expression: print it
O GHCI está nos dizendo que esta expressão produziu uma função do tipo a -> a mas que ele não sabe como apresentar ela na tela. Funções não são instâncias do typeclass Show, então não temos como ter uma representação legal da string de uma função.
Quando rodamos, digamos, 1 + 1 no prompt do GHCI, ele primeiro calcula isso como 2 e então chama show em 2 para receber uma representação em forma de texto deste número. E a representação textual de 2 é justamente a string "2", que é então apresentada na tela.
Alguma altissima-ordem está em ordem
Funções podem receber funções como parâmetros e também retornar funções. Para ilustrar isto, nós vamos fazer uma função que recebe uma função e aplica ela duas vezes em algo!
applyTwice :: (a -> a) -> a -> a applyTwice f x = f (f x)
Antes de mais nada, repare na declaração de tipo. Antes, nós não precisavamos de parênteses porque -> é naturalmente associativa à direita. Entretando, aqui, eles são obrigatórios. Eles indicam que o primeiro parâmetro é uma função que recebe algo e retorna esta mesma coisa. O segundo parâmetro é algo deste tipo também e o valor de retorno é também do mesmo tipo. Nós também poderíamos ler esta declaração de uma forma mais curried, mas para nos poupar desta dor de cabeça, nós vamos apenas dizer que esta função recebe dois parâmetros e retorna uma coisa. O primeiro parâmetro é uma função (do tipo a -> a) e o segundo é o próprio a. A função pode ser também Int -> Int ou String -> String ou qualquer outra coisa. Neste caso, o segundo parâmetro também deverá ser deste tipo.
O corpo da função é bem simples. Apenas usamos o parâmetro f como uma função, aplicando x à ela ao separá-los com um espaço e então aplicando o resultado a f novamente. De qualque modo, brincando com a função:
ghci> applyTwice (+3) 10
16
ghci> applyTwice (++ " HAHA") "HEY"
"HEY HAHA HAHA"
ghci> applyTwice ("HAHA " ++) "HEY"
"HAHA HAHA HEY"
ghci> applyTwice (multThree 2 2) 9
144
ghci> applyTwice (3:) [1]
[3,3,1]
Fica evidente o quão legal e útil é a aplicação parcial. Se a nossa função requer que passemos à ela uma função que recebe apenas um parâmetro, nós podemos apenas aplicar parcialmente uma função no ponto onde se recebe apenas um parâmetro e então passá-lo.
Agora nós vamos usar programação de alta ordem para implementar uma função realmente útil que está na biblioteca padrão. Ela se chama zipWith. Ela recebe uma função e duas listas como parâmetros e então junta as duas listas aplicando a função entre os elementos correspondentes. Aqui está como nós vamos implementá-la:
zipWith' :: (a -> b -> c) -> [a] -> [b] -> [c] zipWith' _ [] _ = [] zipWith' _ _ [] = [] zipWith' f (x:xs) (y:ys) = f x y : zipWith' f xs ys
Olhe a declaração do tipo. O primeiro parâmetro é uma função que recebe duas coisas e produz uma terceira. Elas não precisam ser do mesmo tipo, mas podem. O segundo e o terceiro parâmetros são listas. O resultado é também uma lista. O primeiro tem que ser uma lista de as, porque a função de junção recebe as como primeiros argumentos. A segunda tem que ser uma lista de bs, porque o segundo argumento da função é do tipo b. O resultado é uma lista de cs. Se a declaração do tipo de uma função diz que ela aceita uma função a -> b -> c como parâmetro, ela também aceitará uma função a -> a -> a, mas não o contrário! Lembre-se de que, quando você está fazendo funções, especialmente as de alta ordem, e você não está seguro sobre o tipo, você pode simplesmente tentar omitir a declaração do tipo e então verificar o que o Haskell infere que seja, usando :t.
A ação na função é bem parecida com a zip normal. As condições limite são as mesmas, mas há um argumento extra, qual seja, a função de junção, mas este argumento não importa nas condições limite, então usamos um _ para ele. E o corpo da função no último pattern é também parecido com zip, mas ele não faz (x,y), e sim f x y. Uma única função de alta ordem pode ser usada para uma enorme variedade de tarefas se é suficientemente geral. Aqui está uma pequena demonstração de todas as diferentes coisas que a nossa função zipWith' é capaz de fazer:
ghci> zipWith' (+) [4,2,5,6] [2,6,2,3] [6,8,7,9] ghci> zipWith' max [6,3,2,1] [7,3,1,5] [7,3,2,5] ghci> zipWith' (++) ["foo ", "bar ", "baz "] ["fighters", "hoppers", "aldrin"] ["foo fighters","bar hoppers","baz aldrin"] ghci> zipWith' (*) (replicate 5 2) [1..] [2,4,6,8,10] ghci> zipWith' (zipWith' (*)) [[1,2,3],[3,5,6],[2,3,4]] [[3,2,2],[3,4,5],[5,4,3]] [[3,4,6],[9,20,30],[10,12,12]]
Como você pode ver, uma única função de alta ordem pode ser usada de modos muito versáteis. A programação imperativa utiliza normalmente coisas como iterações com for, iterações com while, setar algo à uma variável, verificar seu estado, e etc., para atingir um certo comportamento e então envolve isso em uma interface, como em uma função. Já a programação funcional, utiliza funções de alta ordem para abstrair padrões comuns, como examinar duas listas aos pares e fazer algo nestes pares ou receber um conjunto de soluções e eliminar as que você não precisa.
Nós vamos implementar outra função que também já está na biblioteca padrão, chamada flip. Flip simplesmente recebe uma função e retorna uma função que é parecida com a função original mas cujos primeiros dois argumentos são invertidos. Nós podemos implementá-la assim:
flip' :: (a -> b -> c) -> (b -> a -> c)
flip' f = g
where g x y = f y x
Lendo a declaração do tipo, nós dizemos que ela recebe uma função que recebe um a e um b e retorna uma função que recebe um b e um a. Mas justamente porque funções são curried por padrão, o segundo par de parênteses é na verdade desnecessário, porque -> é associativo à direita por padrão. (a -> b -> c) -> (b -> a -> c) é o mesmo que (a -> b -> c) -> (b -> (a -> c)), e que é o mesmo que (a -> b -> c) -> b -> a -> c. Nós escrevemos que g x y = f y x. Se isso é verdade, então f y x = g x y também deve ser, certo? Tendo isso em mente, nós podemos definir esta função de uma forma ainda mais simples.
flip' :: (a -> b -> c) -> b -> a -> c flip' f y x = f x y
Aqui, nós tiramos vantagem do fato de que funções são curried. Quando nós chamamos flip' f sem os parâmetros x e y, ela vai retornar uma f que recebe esses dois parâmetros, mas que os chama invertidos. Mesmo que funções invertidas sejam normalmente passadas para outras funções, nós tiramos vantagem do currying quando fazemos funções de alta ordem pensando adiante e escrevendo como o seu resultado final seria se ela fosse chamada totalmente aplicada.
ghci> flip' zip [1,2,3,4,5] "hello"
[('h',1),('e',2),('l',3),('l',4),('o',5)]
ghci> zipWith (flip' div) [2,2..] [10,8,6,4,2]
[5,4,3,2,1]
Mapas e filtros
map recebe uma função e uma lista e aplica esta função em todos elementos da lista, produzindo uma nova lista. Vamos ver como é a sua declaração de tipo e como ele é definido.
map :: (a -> b) -> [a] -> [b] map _ [] = [] map f (x:xs) = f x : map f xs
A declaração de tipo nos diz que esta função recebe um a e retorna um b, uma lista de a's e retorna uma lista de b's. O interessante aqui é dar uma olhada na assinatura de tipos da função, algumas vezes só olhando isso você já consegue saber como ela funciona. map é realmente uma das mais versáteis funções de ordem superior que poderemos utilizar em milhares de formas diferentes. Veja ela em ação:
ghci> map (+3) [1,5,3,1,6] [4,8,6,4,9] ghci> map (++ "!") ["BIFF", "BANG", "POW"] ["BIFF!","BANG!","POW!"] ghci> map (replicate 3) [3..6] [[3,3,3],[4,4,4],[5,5,5],[6,6,6]] ghci> map (map (^2)) [[1,2],[3,4,5,6],[7,8]] [[1,4],[9,16,25,36],[49,64]] ghci> map fst [(1,2),(3,5),(6,3),(2,6),(2,5)] [1,3,6,2,2]
Você provavelmente já sabe que cada um deles pode ser realizado com uma compreensão de lista. map (+3) [1,5,3,1,6] é o mesmo que escrever [x+3 | x <- [1,5,3,1,6]]. Tanto faz, utilizar map é muito mais legível em muitas situações onde você só pode aplicar alguma função em um elemento da lista, especialmente depois que você estiver lidando com mapas de mapas ter que lidar com uma série de colchetes pode ser um pouco bagunçado.
filter é uma função que recebe um predicado (um predicado é uma função que diz que qualquer coisa é verdadeira ou não, nesse caso, uma função que retorna um valor booleano) e uma lista e então retorna uma lista com elementos que satisfazem o predicado. A declaração de tipo e a implementação é algo como:
filter :: (a -> Bool) -> [a] -> [a]
filter _ [] = []
filter p (x:xs)
| p x = x : filter p xs
| otherwise = filter p xs
Bastante simples. Se p x se transformar em True, o elemento será incluido em uma nova lista. Se isto não acontecer, ficará de fora. Alguns exemplos úteis:
ghci> filter (>3) [1,5,3,2,1,6,4,3,2,1] [5,6,4] ghci> filter (==3) [1,2,3,4,5] [3] ghci> filter even [1..10] [2,4,6,8,10] ghci> let notNull x = not (null x) in filter notNull [[1,2,3],[],[3,4,5],[2,2],[],[],[]] [[1,2,3],[3,4,5],[2,2]] ghci> filter (`elem` ['a'..'z']) "u LaUgH aT mE BeCaUsE I aM diFfeRent" "uagameasadifeent" ghci> filter (`elem` ['A'..'Z']) "i lauGh At You BecAuse u r aLL the Same" "GAYBALLS"
Tudo isto pode ser obtido com uma compreensão de lista e pelo uso de predicados. Não há um conjunto de regras para quando devemos utilizar map e filter ao invés de compreensão de lista, você só deve decidir qual será o mais légível dependendo do código e do contexto. O filter equivale a aplicar diversos predicados em uma compreensão de lista e equivalente a filtrar algo diversas vezes ou juntar o predicado coerentemente com a função &&.
Lembra da função quicksort do capítulo anterior? Utilizamos compreensão de lista para filtrar os elementos que forem menores do que (ou igual a) e maior do que o pivô. Podemos obter a mesma funcionalidade de um jeito mais legível com o uso do filter:
quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
let smallerSorted = quicksort (filter (<=x) xs)
biggerSorted = quicksort (filter (>x) xs)
in smallerSorted ++ [x] ++ biggerSorted
Mapeamento e filtragem é o pão e a manteiga de toda a caixa de ferramentas da programação funcional. Não importa se fizermos isso com map e filter funções ou compreensão de lista. Lembre-se como resolvemos o problema para achar o triângulo retângulo com uma determinada circunferência. Com programação imperativa, nós deveriamos resolvê-lo aninhando três loops e então testando se a combinação atual satisfaz o triângulo retângulo e se tem o perímetro certo. Se fosse este o caso, teríamos que mostrá-lo na tela ou algo assim. Na programação funcional, os padrões são obtidos com mapeamentos e filtragens. Você faz uma função que recebe um valor e produz algum resultado. Nós mapeamos esta função mais uma lista de valores e então nós filtramos o resultado da lista para que os resultados satisfaçam a nossa busca. Graças à preguiça de Haskell, sempre que você mapear algo sobre uma lista várias vezes e filtrá-la várias vezes, ele só irá passar pela lista uma vez.
Vamos encontrar o maior número em 100.000 que é divisível por 3829. Para fazer isso, vamos filtrar um conjunto de possibilidades em que nós sabemos que a solução consiste.
largestDivisible :: (Integral a) => a
largestDivisible = head (filter p [100000,99999..])
where p x = x `mod` 3892 == 0
Primeiro vamos fazer uma lista com todos os números menores do que 100.000, em ordem decrescente. Então vamos filtrá-lo pelo seu predicado e como os números são ordenados de forma decrescente, o maior número que irá satisfazer nosso predicado será o primeiro elemento filtrado da lista. Não precisamos utilizar uma lista infinita para o nosso conjunto inicial. Eis a preguiça em ação novamente. Como nós acabamos utilizando a cabeça da lista filtrada, não importa se a lista filtrada for finita ou infinita. A análise para quando a primeira solução adequada for encontrada.
E agora, nós queremos obter a soma de todos os quadrados ímpares que sejam menores do que 10.000. Primeiramente, como iremos usá-lo em nossa solução, irei introduzir aqui a função takeWhile. Ela recebe um predicado e uma lista e então vai para o inicio da lista e retorna os elementos que satisfazem o predicado. Se o elemento encontrado por ele não satisfazer o predicado, ele para. Se você quer a primeira palavra da string "elefantes é que sabem fazer festa", então faça takeWhile (/=' ') "elefantes é que sabem fazer festa" e ele lhe retornará "elefantes". Beleza. A soma de todos os quadrados ímpares que são menores do que 10.000. Primeiramente, vamos começar mapeando a função (^2) em uma lista infinita [1..]]. Então filtramos somente os ímpares. E agora, vamos pegar os elementos a partir desta lista que tem todos os menores do 10.000. Finalmente, vamos ter a soma de toda essa lista. Nem sempre precisamos definir uma função para isso, vamos fazer direto em uma linha no GHCI:
ghci> sum (takeWhile (<10000) (filter odd (map (^2) [1..]))) 166650
Demais! Começamos com alguns dados iniciais (a lista infinita de todos os números naturais) e então nós mapeamos isto, filtramos e cortamos até que fosse o que precisávamos e depois nós somamos. Também podemos escrever isto utilizando compreensão de lista:
ghci> sum (takeWhile (<10000) [m | m <- [n^2 | n <- [1..]], odd m]) 166650
É uma questão de gosto, escolha a forma que você achar mais bonita. Novamente, a magnífica preguiça do Haskell torna isto possível. Nós podemos mapear e filtrar uma lista infinita, justamente porque ele não mapeia e filtra do jeito convencional, senão essa tarefa seria bem demorada. Somente quando forçamos Haskell a mostrar para nós a soma realizada na função sum é que ele diz para o takeWhile que ele precisa daqueles números. takeWhile força que o mapeamento e a filtragem ocorra, porém somente se algum número maior ou igual do que 10.000 for encontrado.
Nosso próximo problema, será lidar com a sequência de Collatz. Nós pegamos um número. Se ele for par, dividimos por dois. Se for ímpar, dividimos ele por 3 e somamos com mais 1. Pegamos o número resultante e aplicamos a mesma coisa nele, produzindo um novo número e assim por diante. Na essência, nós temos uma sequência de números. Isto é feito para todos os números iniciais, a sequência termina no número 1. Então se tivermos inicialmente o número 13, teremos esta sequência: 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. 13*3 + 1 igual a 40. 40 dividido por 2 é 20, etc. Como vimos a sequência tem 10 termos.
Agora o que nós queremos saber é: para todos os números iniciais entre 1 e 100, quantas sequências tem com um tamanho maior do que 15? Primeiramente, vamos escrever uma função para obter uma sequência:
chain :: (Integral a) => a -> [a]
chain 1 = [1]
chain n
| even n = n:chain (n `div` 2)
| odd n = n:chain (n*3 + 1)
Como a sequência termina em 1, esse seria o caso de limite. Essa é uma função recursiva bem padrão.
ghci> chain 10 [10,5,16,8,4,2,1] ghci> chain 1 [1] ghci> chain 30 [30,15,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2,1]
Feito! Esta funcionando corretamente. E agora, a função para nos dizer a resposta para a nossa questão:
numLongChains :: Int
numLongChains = length (filter isLong (map chain [1..100]))
where isLong xs = length xs > 15
Mapeamos a função chain para [1..100] para obter uma lista das sequências, com eles próprios representando-se como listas. Então os filtramos com o predicado só para verificar se aquelas listas tem o tamanho maior do que 15. Novamente nós filtramos, e conseguimos ver quantas sequências são deixadas na lista resultante.
Usando map, conseguimos fazer também algumas coisas como map (*) [0..], se não por algum motivo que seja então para ilustrar como currying funciona e como funções (parcialmente aplicadas) são valores reais que você pode passar para outra função ou colocar dentro de listas (você só não pode transforma-las em strings). Por enquanto, apenas mapeamos funções que pegam somente um parâmetro sobre uma lista, como map (*2) [0..] que resulta em uma lista do tipo (Num a) => [a], porém podemos fazer também map (*) [0..] sem problemas. O que acontece aqui é que aquele número na lista é aplicado para a função *, que tem o tipo (Num a) => a -> a -> a. Aplicar somente um parâmetro para um função que recebe dois parâmetros, retorna uma função que pega um parâmetro. Se a gente mapear * sobre a lista [0..], vamos ter de volta uma função que pega somente um parâmetro, sendo então (Num a) => [a -> a]. map (*) [0..] produz uma lista igual a que obteriamos se escrevessemos [(0*),(1*),(2*),(3*),(4*),(5*)...
ghci> let listOfFuns = map (*) [0..] ghci> (listOfFuns !! 4) 5 20
Receber o elemento com índice 4 a partir da nossa lista nos retorna uma função equivalente a (4*). Então, apenas aplicamos 5 na função. Que é o mesmo que escrever (4*) 5 ou somente 4 * 5.
Lambdas
Lambdas são basicamente funções anônimas que utilizamos quando precisamos de alguma função uma única vez. Normalmente, criamos um lambda com o propósito único de passá-lo para uma função de ordem superior. Para criar um lambda, digitamos um \ (porque isso se parece com a letra grega lambda caso você seja vesgo o suficiente) e então nós escrevemos os parâmetros separados por espaços. Depois vem o -> e então o corpo da função. Normalmente cercamos com parênteses, porque senão isso se estende para todo o lado direito.
Se você olhar 902px acima, você verá que nós utilizamos uma associação where em nossa função numLongChains para fazer a função isLong com o único propósito de passar isso para o filter. Bem, ao invés de fazermos isso, podemos utilizar um lambda:
numLongChains :: Int numLongChains = length (filter (\xs -> length xs > 15) (map chain [1..100]))
Lambdas são expressões, este é o porque de só passarmos aquilo. A expressão (\xs -> length xs > 15) retorna uma função que nos diz se o length da lista que foi passada é maior do que 15.
Pessoas que não se familiarizaram muito bem antes com o funcionamento de currying e aplicações parciais utilizam lambdas onde não deveriam. Por exemplo, as expressões map (+3) [1,6,3,2] e map (\x -> x + 3) [1,6,3,2] são equivalentes desde que ambos (+3) e (\x -> x + 3) sejam funções que peguem um número e adicione 3 nele. Não preciso dizer que criar um lambda neste caso seria uma estupidez já que com a utilização da aplicação parcial fica bem mais legível.
Assim como uma função normal, lambdas podem receber quantos parâmetros você quiser:
ghci> zipWith (\a b -> (a * 30 + 3) / b) [5,4,3,2,1] [1,2,3,4,5] [153.0,61.5,31.0,15.75,6.6]
E como uma função normal, você pode utilizar um pattern match em lambdas. A única diferença é que você não define alguns patterns para um único parâmetro, como se fizesse um [] e um pattern (x:xs) para o mesmo parâmetro e depois obtesse valores disso. Se um pattern matching falhar em um lambda, um runtime error ocorrerá, portanto seja cuidadoso com pattern matching em lambdas!
ghci> map (\(a,b) -> a + b) [(1,2),(3,5),(6,3),(2,6),(2,5)] [3,8,9,8,7]
Lambdas são normalmente cercadas por parênteses a não ser que você queira estende-la por todo o lado direito. Uma coisa interessante: como funções são curried por default, estes dois são equivalentes:
addThree :: (Num a) => a -> a -> a -> a addThree x y z = x + y + z
addThree :: (Num a) => a -> a -> a -> a addThree = \x -> \y -> \z -> x + y + z
Se definirmos uma função como essa, é óbvio que a declaração de tipo é o que é. Lá estão os -> em ambas declaração de tipo e a equação. Mas é claro, o primeiro jeito de escrever a função é bem mais legível enquanto o segundo é muito mais uma demonstração do modo currying.
Tanto faz, é legal quando utilizamos estas notações. Eu acho que aquela função flip fica bem mais legível quando definimos assim:
flip' :: (a -> b -> c) -> b -> a -> c flip' f = \x y -> f y x
Apesar de isso ser o mesmo que escrever flip' f x y = f y x, fazemos assim obviamente por ser o mais utilizado na criação de uma nova função na maioria dos casos. O caso mais comum na utilização do flip é somente chamá-lo com o parâmetro da função e então passar o resultado para um mapa ou um filtro. Utilize lambdas desse jeito quando você quiser deixar explicito que a sua função é destinada a ser parcialmente aplicada e passada em uma função como um parâmetro.
Somente dobras e cavalos
Anteriormente quando estávamos lidando com recursividade, notamos um tema em comum em várias funções recursivas que trabalham em listas. Normalmente temos um caso extremo para a lista vazia. Introduziremos o padrão x:xs e então faremos algo que envolverá um único elemento e o resto da lista. Este padrão é muito comum, por isso serão introduzidas algumas funções bastante úteis para o entendermos melhor. Estas funções são chamadas de "folds" (livremente traduzidas aqui como dobras). Elas são como a função map, só que reduzem a lista em um valor único.
Uma "fold" recebe uma função binária, com um valor inicial (gosto de chamá-lo de acumulado) e uma lista que será dobrada em diversas etapas até se tornar uma dobra única. A função binária tem dois parâmetros. A função binária é chamada com o valor acumulado e o primeiro (ou último) elemento e produz um novo acumulador. Então a função binária é chamada novamente com o novo valor acumulado e agora com o novo primeiro (ou último) elemento, e assim por diante. Uma vez percorrida toda a lista apenas o valor acumulado permanece, que é o que sobra da lista que reduzimos.
Primeiro vamos dar uma olhada na função foldl, também chamada de "left fold" (dobra esquerda). Isto dobra a lista a partir do lado esquerdo. A função binária é aplicada entre o valor inicial e a cabeça da lista. Isto produzirá um novo valor acumulado e a função binária será chamada com este valor e o próximo elemento, etc.
Vamos implementar novamente o sum, só dessa vez, utilizando o fold no lugar da recursão.
sum' :: (Num a) => [a] -> a sum' xs = foldl (\acc x -> acc + x) 0 xs
Testando, um dois três:
ghci> sum' [3,5,2,1] 11
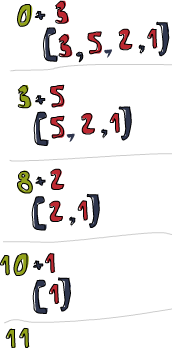
Vamos dar uma olhada melhor em como esta "dobra" funciona. \acc x -> acc + x é a função binária. 0 é o valor inicial e xs é a lista a ser dobrada. Primeiramente, 0 é usado sendo o parâmetro acc na função binária e 3 é usado como sendo o parâmetro x (ou o elemento atual).0 + 3 produzirá um 3 e será o novo valor do acumulador, como já foi dito. Logo depois, 3 será usado como sendo o valor acumulado e 5 como sendo o elemento atual e 8 passa a ser o novo valor acumulado. Indo adiante, 8 é o novo valor acumulado, 2 é o elemento atual, então o valor do novo elemento acumulado será 10. Finalmente, aquele 10 é utilizado como o valor acumulado e 1 é o elemento atual, produzindo um 11. Parabéns, você fez uma dobra!
Este diagrama profissional a sua esquerda ilustra como a dobra acontece, passo a passo (a cada momento!). O número verde escuro é o valor acumulado. Você pode ver como a lista é ordenada e consumida de cima a partir da esquerda pelo acumulador. Aeee ae ae ae! Se levarmos em conta que aquela função é curried, poderemos escrever esta implementação mais sucintamente dessa maneira:
sum' :: (Num a) => [a] -> a sum' = foldl (+) 0
A função lambda (\acc x -> acc + x) é o mesmo que (+). Nós podemos omitir que o xs é um parâmetro porque chamar foldl (+) 0 irá retornar uma função com uma lista. Geralmente, se você tem uma função como foo a = bar b a, você poderá reescreve-la como foo = bar b, por causa do currying.
Vamos implementar outra função com a dobra esquerda e depois com dobras a direita. Tenho certeza que todos vocês já sabem que aquele elem verifica qualquer valor que seja parte de uma lista, então não vou introduzir isto novamente (epa, só falei!). Vamos implementar isto com a dobra esquerda.
elem' :: (Eq a) => a -> [a] -> Bool elem' y ys = foldl (\acc x -> if x == y then True else acc) False ys
Bem, bem, bem, o que fizemos aqui? O valor inicial e o acumulado aqui são um valor booleano. O tipo do valor acumulado e o resultado final são sempre os mesmos quando lidamos com dobras. Lembre-se disso se você ainda não sacou como é usado o valor inicial, isto pode te dar uma idéia. Começamos com False. Isto faz sentido se usarmos False como valor inicial. Nós assumimos que ele não esta lá. Outra coisa, se chamarmos uma dobra em uma lista vazia, o resultado será somente o valor inicial. Então vamos verificar se o elemento inicial é o elemento que estamos procurando. Se for, setamos o acumulado como True. Se não, nós simplesmente não mudamos o valor acumulado. Se ele já for False permanecerá assim porque o elemento atual não é isso. Se ele for True, saímos por lá.
A dobra a direita foldr, funciona de forma similar a dobra esquerda, só que o acumulador começa a consumir os valores a partir da direita. Além disso, funções binárias com dobra esquerda tem o seu acumulador como o primeiro parâmetro e o valor atual sendo o segundo (como \acc x -> ...), as funções binárias com dobra direita tem como valor atual o primeiro parâmetro e o acumulador o segundo (como \x acc -> ...). Isto só fará sentido se essa dobra direita tiver o acumulador na direita, porque isso irá dobrar a partir do lado direito.
O valor acumulado (e por isso, o resultado) da dobra pode ter qualquer tipo. Ele pode ser um número, um booleano ou também uma nova lista. Vamos implementar a função map com a dobra a direita. O acumulador deverá ser uma lista, que iremos acumulando e mapeando a lista elemento por elemento.
map' :: (a -> b) -> [a] -> [b] map' f xs = foldr (\x acc -> f x : acc) [] xs
Se nós mapearmos (+3) em [1,2,3], acessaremos a lista a partir do lado direito. Pegamos o último elemento, que é 3 e aplicamos a função nele, que no final será 6. Então, nós acrescentamos isto no valor acumulado, que será []. 6:[] é [6] e é agora o valor acumulado. Nós aplicamos (+3) ao 2, que será 5 e acrescentamos (:) isto ao acumulado, então o valor acumulado será agora [5,6]. Aplicamos (+3) ao 1 e acrescentamos ele ao acumulado e então o valor final será [4,5,6].
É claro, vamos querer implementar esta função com a dobra a esquerda também. Isto poderá ser map' f xs = foldl (\acc x -> acc ++ [f x]) [] xs, porém a idéia é que aquela função ++ seja muito mais custosa do que :, então normalmente utilizamos dobras a direita quando nós queremos construir novas listas a partir de uma lista.
Se você reverter a lista, você poderá fazer a dobra direita do mesmo modo que fazemos a dobra esquerda e vice-versa. Algumas vezes você não tem como fazer isso. A função sum pode ser implementada muito bem do mesmo jeito com uma dobra esquerda e direita. A grande diferença é que a dobra direita funciona em listas infinitas, ao contrario da esquerda que não! Para esclarecer melhor, se você pegar uma lista infinita a partir de um ponto e você dobrá-la a partir da direita, você irá eventualmente descobrir o início da lista. Entretanto, se você quiser pegar uma lista infinita a partir de um ponto e tentar dobrá-la a partir da esquerda, você nunca chegará no fim!
Dobras podem ser usadas para implementar qualquer função onde você percorre uma lista uma única vez, elemento por elemento, e então retorna algo baseado nisso. Sempre que você quiser percorrer uma lista para retornar alguma coisa, é provável que você queira uma dobra. Por isso que dobras vem com mapas e filtros, um dos tipos mais úteis de funções na programação funcional.
As funções foldl1 e foldr1 funcionam da mesma forma que foldl e foldr, só que você não precisa informar explicitamente qual o valor inicial. Ela assume que o primeiro (ou último) elemento da lista é o valor inicial da dobra e então inicia a dobra com ele. Com isto em mente, a função sum pode implementar algo como: sum = foldl1 (+). Como eles dependem de pelo menos um elemento para dobrar a lista, isto causará um runtime error caso seja chamado com uma lista vazia. Por outro lado, foldl e foldr trabalham bem com listas vazias. Quando criar uma dobra, pense sobre como isso irá se comportar com uma lista vazia. Se a função não fizer sentido quando tiver uma lista vazia, você provavelmente usará foldl1 ou foldr1 para implementar isso.
Só para te mostrar como dobras são poderosas, vamos implementar algumas funções da biblioteca padrão utilizando dobras:
maximum' :: (Ord a) => [a] -> a maximum' = foldr1 (\x acc -> if x > acc then x else acc) reverse' :: [a] -> [a] reverse' = foldl (\acc x -> x : acc) [] product' :: (Num a) => [a] -> a product' = foldr1 (*) filter' :: (a -> Bool) -> [a] -> [a] filter' p = foldr (\x acc -> if p x then x : acc else acc) [] head' :: [a] -> a head' = foldr1 (\x _ -> x) last' :: [a] -> a last' = foldl1 (\_ x -> x)
head e last são implementadas melhor pelo uso de pattern matching, mas só para ver, você pode obte-los através do uso de dobras. Nossa definição de reverse' é bastante clara, eu acho. Nós temos um valor inicial de uma lista vazia e então acessamos nossa lista a partir da esquerda e vamos adicionamos ao nosso valor acumulado. No final, nós construímos uma lista reversa. \acc x -> x : acc assemelhasse a função :, somente os parâmetros são movimentados. Este é o porque que poderíamos ter escrito nosso reverse como foldl (flip (:)) [].
Outro jeito para esboçar a dobra direita e a esquerda é algo como: digamos que temos uma dobra direita e uma função binária f com um valor inicial z. Se formos dobrar a lista [3,4,5,6], essencialmente faremos isso: f 3 (f 4 (f 5 (f 6 z))). f é chamado com o último elemento da lista e o valor acumulado, este valor é dado ao valor acumulado para o próximo último valor e assim por diante. Se nós fizermos o f ser + e o valor acumulado inicial ser 0, aquilo ficará 3 + ( 4 + ( 5 + (6 +0 ) ) ) . Ou se nós colocarmos o + como uma função prefixo, aquilo ficaria então (+) 3 ((+) 4 ( (+) 5 ( (+) 6 0) ) ). De forma similar, fazemos a dobra esquerda com uma lista g com flip (:) sendo a função binária e [] o valor acumulado (então reverteríamos a lista), isto seria o equivalente a flip (:) (flip (:) (flip (:) (flip (:) [] 3) 4) 5) 6. E certamente, se executarmos esta expressão, teríamos [6,5,4,3].
scanl e scanr são como foldl e foldr, eles só informam todos os estados intermediários do valor acumulado na forma de uma lista. Há também o scanl1 e scanr1, que são idênticos ao foldl1 e foldr1.
ghci> scanl (+) 0 [3,5,2,1] [0,3,8,10,11] ghci> scanr (+) 0 [3,5,2,1] [11,8,3,1,0] ghci> scanl1 (\x acc -> if x > acc then x else acc) [3,4,5,3,7,9,2,1] [3,4,5,5,7,9,9,9] ghci> scanl (flip (:)) [] [3,2,1] [[],[3],[2,3],[1,2,3]]
Quando usamos o scanl, o resultado final estará no último elemento da lista resultante enquanto o scanr irá colocar o resultado no primeiro.
Scans são usadas para monitorar a progressão de uma função que pode ser implementada como uma dobra. Vamos responder essa nossa questão: Quantos elementos precisamos ter para somar a raiz de todos os números naturais que excedem 1000?. Para obter o quadrado de todos os números naturais, nós temos que fazer map sqrt [1..]. Agora, para ter a soma, nós temos que fazer uma dobra, mas como nós temos interesse em como a soma irá progredir, faremos usando o scan. Uma vez tendo feito o scan, podemos ver quantas somas estão sob 1000. A primeira soma no resultado do scanlist será normalmente 1. O segundo será 1 mais a raiz quadrada de 2. O terceiro será a soma da raiz quadrada de 3. Se estas X somas estiverem abaixo de 1000, então somamos X+1 dos que excederem 1000.
sqrtSums :: Int sqrtSums = length (takeWhile (<1000) (scanl1 (+) (map sqrt [1..]))) + 1
ghci> sqrtSums 131 ghci> sum (map sqrt [1..131]) 1005.0942035344083 ghci> sum (map sqrt [1..130]) 993.6486803921487
Usamos aqui takeWhile no lugar de filter porque filter não trabalha com listas infinitas. Apesar de sabermos que a lista é ascendente, filter não faz assim, então usamos takeWhile para terminar o scanlist na primeira ocorrência da soma maior do que 1000.
Aplicação de Função com $
Beleza, agora vamos dar uma olhada na função $, também chamada de aplicação de função. Antes de qualquer coisa, vamos ver como isto é definido:
($) :: (a -> b) -> a -> b f $ x = f x
Que negócio é esse? Qual a utilidade desse operador? Ele nada mais é do que uma aplicação de função! Bem, quase foi agora, mas não muito! Enquanto uma aplicação de função normal (que coloca um espaço entre duas coisas) tem realmente uma alta precedência, a função $ tem baixa precedência. Aplicar função com um espaço associa à esquerda (ou seja, f a b c é o mesmo que ((f a) b) c))), aplicar função com $ associa à direita.
Isto tudo é muito bacana, mas como isso irá me ajudar? Na maioria dos casos, esta é uma função conveniente, ou seja, nós não precisamos escrever muitos parênteses. Considere a expressão sum (map sqrt [1..130]). Como $ tem baixa precedência nós podemos reescrever esta expressão como sum $ map sqrt [1..130], salvando nós mesmo de preciosas teclas não digitadas! Quando um $ é encontrado, a expressão a sua direita é aplicada como um parâmetro da função a sua esquerda. Como seria sqrt 3 + 4 + 9? Isto soma juntos 9, 4 e a raiz quadrada de 3. Se quisermos a raiz quadrada de 3 + 4 + 9, temos que escrever sqrt (3 + 4 + 9) ou se usarmos $ podemos escrever como sqrt $ 3 + 4 + 9 porque $ tem a menor precedência sobre qualquer operador. Este é o porque que você deve imaginar um $ como sendo uma espécie do equivalente a escrever um parênteses para abrir e outro para fechar na direita da sua expressão.
E como seria sum (filter (> 10) (map (*2) [2..10]))? Bem, como $ associa à direita, f (g (z x)) é igual a f $ g $ z x. E então nós pode reescrever sum (filter (> 10) (map (*2) [2..10])) como sum $ filter (> 10) $ map (*2) [2..10]
Mas além de nos livrar de parênteses, $ significa que a aplicação de função pode ser tratada como apenas outra função. Dessa forma, nós podemos, por exemplo, mapear a aplicação de função em uma lista de funções.
ghci> map ($ 3) [(4+), (10*), (^2), sqrt] [7.0,30.0,9.0,1.7320508075688772]
Composição de funções
Na matemática, composição de funções é definida como: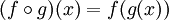 
, que significa que compor duas funções produz uma nova função, quando chamamos com um parâmetro, digamos, x é o equivalente a chamar g com o parâmetro x e então chamar o f com aquele resultado.
Em Haskell, composição de funções é praticamente a mesma coisa. Fazemos uma composição de funções com a função ., que é definida como:
(.) :: (b -> c) -> (a -> b) -> a -> c f . g = \x -> f (g x)
Atente na declaração de tipo. f deve ter como parâmetro um valor com o mesmo tipo do valor retornado de g. Assim, a função resultante assume um parâmetro do mesmo tipo daquele g que assume e retorna um valor do mesmo tipo que f retorna. A expressão negate . (* 3) retorna uma função que pega um número, multiplica ele por 3 e então faz a negação.
Um dos usos da composição de funções é fazer funções em tempo de execução para passar para outras funções. Claro, nós podemos usar lambdas para isso, mas muitas vezes, composição de funções é mais clara e concisa. Digamos que temos uma lista de números e nós queremos então tornar todos em números negativos. Uma forma para fazer isto seria pegar cada número com valor absoluto e então negá-lo, como isso:
ghci> map (\x -> negate (abs x)) [5,-3,-6,7,-3,2,-19,24] [-5,-3,-6,-7,-3,-2,-19,-24]
Observe a lambda e como ela se parece com o resultado da composição da função. Usando composição de função, podemos reescrever isto como:
ghci> map (negate . abs) [5,-3,-6,7,-3,2,-19,24] [-5,-3,-6,-7,-3,-2,-19,-24]
Fabuloso! Composição de funções é associativo à direita, então nós podemos compor muitas funções ao mesmo tempo. A expressão f (g (z x)) é o equivalente a (f . g . z) x. Com isso em mente, podemos transformar isto
ghci> map (\xs -> negate (sum (tail xs))) [[1..5],[3..6],[1..7]] [-14,-15,-27]
nisso
ghci> map (negate . sum . tail) [[1..5],[3..6],[1..7]] [-14,-15,-27]
Mas e quando funções têm muitos parâmetros? Bem, se você quiser usar na composição de funções, terá que aplicar parcialmente cada função pegando apenas um parâmetro. sum (replicate 5 (max 6.7 8.9)) pode ser reescrita como (sum . replicate 5 . max 6.7) 8.9 ou como sum . replicate 5 . max 6.7 $ 8.9. O que acontece aqui é: uma função que pega o resultado de max 6.7 e aplica em replicate 5. Em seguida, a função pega o resultado disso e não a soma do que é criado. Finalmente, a função é chamada com 8.9. Mas normalmente, você lê isso como: aplique 8.9 em max 6.7, então aplique replicate 5 e depois aplique sum. Se você quiser reescrever essa expresão com alguns parênteses usando composição de funções, você pode começar colocando o último parâmetro na função mais interna após um $ e depois compor todas as outras chamadas de funções, escrevendo sem o último parâmetro e colocando pontos entre eles. Se você tiver replicate 100 (product (map (*3) (zipWith max [1,2,3,4,5] [4,5,6,7,8]))), você pode escrever isso como replicate 100 . product . map (*3) . zipWith max [1,2,3,4,5] $ [4,5,6,7,8]. Se a função terminar com uma árvore de parânteses, são grandes as chances de você traduzir em uma composição de função, que terá três operadores de composição.
Outro uso comum da composição de função é definir funções em um estilo chamado de 'ponto livre'. Pegue como exemplo esta função que escrevemos anteriormente:
sum' :: (Num a) => [a] -> a sum' xs = foldl (+) 0 xs
O xs é exposto em ambos os lados. Por causa do currying, nós podemos omitir o xs em ambos os lados, porque chamar foldl (+) 0 cria uma função que pega uma lista. Escrevendo a função como sum' = foldl (+) 0 é o que se chama de escrever com o estilo ponto livre. Como podemos escrever isso no estilo ponto livre?
fn x = ceiling (negate (tan (cos (max 50 x))))
Não podemos simplesmente se livrar do x em ambos os lados. O x no corpo da função esta entre parênteses. cos (max 50) não faz sentido. Você não obtém o cosseno da função. O que podemos fazer é expressão fn com uma composição de funções.
fn = ceiling . negate . tan . cos . max 50
Excelente! Muitas vezes, o estilo ponto livre é mais legível e conciso, porque ele faz você pensar sobre as funções e o que cada função que compõe os resultados fazem ao invés de pensar sobre os dados e como eles são embaralhados. Você pode pegar funções simples e usar composição como cola para tornar mais complexa. Tanto faz, usar o estilo ponto livre pode se tornar menos legível se a função for muito complexa. Por isso que não é recomendado fazer longas composições de funções, apesar de eu me declarar culpado por usar composição muitas vezes. O estilo preferencial é usar uma associação let para rotular resultados intermediários ou juntar o problema em subproblemas e depois colocá-los juntos para que a função faça sentido para que alguém que irá ler ao invés de fazer uma longa cadeia de composições.
Na sessão sobre mapas e filtros, resolvemos um problema encontrando a soma de todos os quadrados ímpares que são menores do que 10.000. Veja como fica a solução quando colocamos isso na função.
oddSquareSum :: Integer oddSquareSum = sum (takeWhile (<10000) (filter odd (map (^2) [1..])))
Sendo um grande fã de composição de função, provavelmente eu teria escrito assim:
oddSquareSum :: Integer oddSquareSum = sum . takeWhile (<10000) . filter odd . map (^2) $ [1..]
No entanto, se tiver alguma chance de outra pessoa ler esse código, eu escreveria então assim:
oddSquareSum :: Integer
oddSquareSum =
let oddSquares = filter odd $ map (^2) [1..]
belowLimit = takeWhile (<10000) oddSquares
in sum belowLimit
Eu não iria ganhar nenhuma competição de golfe com esse código, mas qualquer um que ler a função provavelmente vai achar mais fácil ler isso do que uma cadeia de composição.