Recursão

Olá recursão!

Nós já mencionamos recursão brevemente no capítulo anterior. Nesse capítulo, veremos recursão mais de perto, porque ela é importante em Haskell por nos permitir construir soluções muito concisas e elegantes para problemas pensando recursivamente.

Se você ainda não sabe o que é recursão, leia essa frase do ínicio novamente. Hahaha! Estou só brincando! Recursão é na verdade uma forma de definir funções onde ela própria é usada em sua definição. Geralmente definições em matemática são dadas recursivamente. Por exemplo, a sequência Fibonacci é definida recursivamente. Primeiro, definimos explicitamente os primeiros dois números de Fibonacci. Dizemos que F(0) = 0 e F(1) = 1, o que significa que o 0-ésimo e primeiro números de Fibonacci são 0 e 1, respectivamente. Então dizemos que, para qualquer outro número natural, aquele número de Fibonacci será a soma dos dois números de Fibonacci anteriores. Então F(n) = F(n-1) + F(n-2). Dessa forma, F(3) é F(2) + F(1), que é (F(1) + F(0)) + F(1). Como nós agora chegamos a somente números de Fibonacci definidos não-recursivamente, nós podemos seguramente dizer que F(3) é 2. Um ou dois elementos definidos não-recursivamente numa definição recursiva (como F(0) e F(1) aqui) são chamados também de condições limites e são importantes caso você queira que sua função recursiva termine em algum momento. Se não tivéssemos definido F(0) e F(1) não-recursivamente, você nunca encontraria número algum na solução, já que chegaria ao 0 e então continuaria nos números negativos. De repente, você estaria dizendo que F(-2000) é F(-2001) + F(-2002) e ainda assim não haveria um fim à vista!

Recursão é importante em Haskell porque, diferentemente das linguagens imperativas, você faz computações em Haskell declarando o que alguma coisa é ao invés de declarar como você chegou a ela. Por essa razão não há laços while ou for em Haskell. Por isso muitas vezes temos que usar recursão para declarar o que alguma coisa é.

Maior do melhor

A função maximum recebe uma lista de coisas que podem ser ordenadas (por exemplo, instâncias da typeclass Ord) e retorna a maior delas. Pense em como você implementaria isso de forma imperativa. Provavelmente você criaria uma variável para guardar o valor máximo encontrado até então e aí percorreria cada um dos elementos da lista. Caso um elemento fosse maior que o máximo, você o substituiria pelo anterior. O máximo que permanecesse ao fim seria o resultado. Ei! Foram bastante palavras para definir um algoritmo tão simples!

Agora vamos pensar em como definiríamos isso recursivamente. Poderíamos já dizer que o maior número de uma lista com um elemento é ele próprio. Então que o maior de uma lista com mais de um elemento é o primeiro elemento, caso este seja maior que o maior do resto. Se for o maior do resto, bem, então será ele. Isso! Agora vamos implementar em Haskell.

maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs)
    | x > maxTail = x
    | otherwise = maxTail
    where maxTail = maximum' xs

Como você pode ver, pattern matching e recursão formam uma grande dupla! A maioria das linguagens imperativas não tem pattern matching, o que leva você a criar muitas estruturas if/else para testar as condições limites. Aqui, nós simplesmente as colocamos como patterns. Então a primeira condição limite diz que se uma lista está vazia, crash! Faz sentido porque qual é o maior elemento de um lista vazia? Eu não sei. O segundo pattern também funciona como uma condição limite. Ele diz que se a lista tem apenas um único elemento, devemos apenas retorná-lo.

Agora, no terceiro pattern é onde a ação acontece. Nós usamos pattern matching para dividir a lista em primeiro elemento e resto. Usamos também uma associação where para definir maxTail como o maior do resto da lista. Então nós testamos se o primeiro é maior que maxTail. Se for, nós retornamos ele. Se não, retornamos maxTail.

Peguemos o exemplo de uma lista de números e vejamos como isso funcionaria neles: [2,5,1]. Se chamarmos maximum' com ela, os primeiros dois patterns não vão ser encontrados. O terceiro irá e a lista então será dividida em 2 e [5,1]. A cláusula where tem o objetivo de descobrir o maior de [5,1], e então nós seguimos por aí. Ela testa o terceiro pattern novamente e [5,1] é dividido em 5 e [1]. Novamente, a cláusula where quer saber o maior de [1]. Como essa é a condição limite, ela retorna 1. Finalmente! Então voltando um grau de execução, comparamos 5 com o maior de [1] (que é 1) e chegamos a 5. Então agora já sabemos que o maior de [5,1] é 5. Subimos novamente, onde tínhamos 2 e [5,1]. Comparando 2 com o maior de [5,1] (5), nós escolhemos o 5.

Uma forma ainda mais clara de escrever essa função seria com max. Caso se lembre dela, max é uma função que pega dois números e retorna o maior deles. Aqui está como nós poderíamos reescrever maximum' usando max:

maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs) = max x (maximum' xs)

Quanta sofisticação! Em essência, o maior elemento de uma lista é o maior entre o primeiro e o maior do resto da lista.

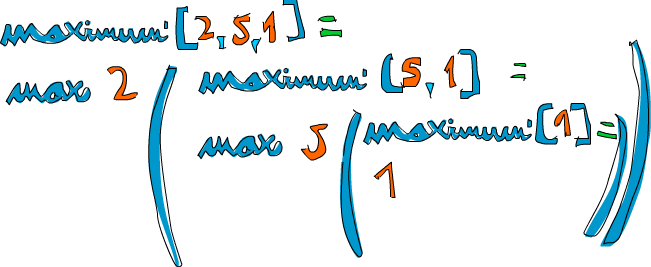
Um pouco mais de funções recursivas

Agora que já sabemos como pensar recursivamente, vamos implementar algumas funções usando recursão. Primeiramente, vamos implementar replicate. replicate recebe um Int junto de algum elemento e retorna uma lista com várias repetições do mesmo elemento. Por exemplo replicate 3 5 retorna [5,5,5]. Pensemos sobre a condição limite. Meu palpite é de que a condição limite seja 0 ou menos. Se tentarmos replicar alguma coisa zero vezes, devemos retornar uma lista vazia. O mesmo para números negativos, porque isso não faria sentido.

replicate' :: (Num i, Ord i) => i -> a -> [a]
replicate' n x
    | n <= 0    = []
    | otherwise = x:replicate' (n-1) x

Aqui usamos guards em vez de patterns porque estamos interessados em uma condição booleana. Se n é menor ou igual a 0, retorna uma lista vazia. Se não, retorna uma lista que tem x como primeiro elemento e então x replicado n-1 vezes como a cauda (se tratando de listas e algoritmos, a nomenclatura cabeça e cauda é bastante usada, acostume-se). Eventualmente, a parte (n-1) fará com que a função chegue à nossa condição limite.

Em seguida, vamos implementar take, que retorna um certo número de elementos de uma lista. Por exemplo, take 3 [5,4,3,2,1] retornando [5,4,3]. Se tentarmos pegar 0 ou menos elementos de uma lista, receberemos uma lista vazia. Também, se tentamos pegar algo de uma lista vazia, receberemos uma lista vazia. Note que essas são as duas condições limite. Então, vamos implementar a função:

take' :: (Num i, Ord i) => i -> [a] -> [a]
take' n _
    | n <= 0   = []
take' _ []     = []
take' n (x:xs) = x : take' (n-1) xs

O primeiro pattern define que se tentarmos pegar 0 ou um número negativo de elementos, vamos receber a lista vazia. Note que estamos usando _ para comparar com a lista porque não nos interessamos pelo seu valor nesse caso. Note também que nós usamos um guard, mas sem o otherwise. Isso significa que se n for maior do que 0, o pattern matching irá para o próximo pattern. O segundo pattern indica que, se tentarmos pegar alguma coisa de uma lista vazia, vamos receber uma lista vazia. O terceiro pattern quebra a lista em uma cabeça e uma cauda. E então nós dizemos que pegar n elementos de uma lista é igual a uma lista que tem x como a cabeça e então uma outra lista que pega n-1 elementos da cauda como cauda. Tente usar um pedaço de papel para escrever como o algoritmo funcionaria em, digamos, 3 de [4,3,2,1].

reverse simplesmente inverte uma lista. Pense sobre a condição limite. O que ela seria? Vamos lá... é a lista vazia! Uma lista vazia invertida é igual à própria lista vazia. Legal. E o resto? Bem, você poderia dizer que se dividirmos uma lista em cabeça e cauda, a lista invertida é igual à cauda invertida com a cabeça no final.

reverse' :: [a] -> [a]
reverse' [] = []
reverse' (x:xs) = reverse' xs ++ [x]

E aí está pronto.

Como Haskell aceita listas infinitas, nossa recursão não necessariamente precisa ter uma condição limite. Mas se não tiver, nós ou ficaremos repetindo algo infinitamente ou vamos produzir uma estrutura de dados infinita, como uma lista infinita. O lado bom das listas infinitas é que nós podemos cortá-las onde quisermos. repeat pega um elemento e retorna uma lista infinita que tem apenas aquele elemento. Uma implementação recursiva disso é realmente fácil. Olhe:

repeat' :: a -> [a]
repeat' x = x:repeat' x

Chamar repeat 3 nos dará uma lista que começa com 3 e então tem uma quantidade infinita de 3 como cauda. Então chamar repeat 3 resuta em algo como 3:repeat 3, que é 3:(3:repeat 3), que é 3:(3:(3:repeat 3)). repeat 3 nunca terminará o pattern matching, enquanto take 5 (repeat 3) nos retornará uma lista de cinco 3's. Então, essencialmente, é o mesmo que fazer replicate 5 3.

zip pega duas listas e mescla elas. zip [1,2,3] [2,3] retorna [(1,2),(2,3)], porque ela trunca a lista maior para combinar com o tamanho da lista menor. E se a gente chamar zip passando uma lista vazia? Bem, vamos receber então, uma lista vazia. Essa então será a nossa condição limite. Contudo, zip pega duas listas como parâmetro, e assim haverá duas condições limite.

zip' :: [a] -> [b] -> [(a,b)]
zip' _ [] = []
zip' [] _ = []
zip' (x:xs) (y:ys) = (x,y):zip' xs ys

Os primeiros dois patterns dizem que se a primeira ou segunda lista é vazia, nós pegamos uma lista vazia. O terceiro diz que a chamada de zip em duas listas é igual a parear as suas cabeças e então continuar a chamar zip nas caudas. A chamada de zip nas listas [1,2,3] e ['a','b'] eventualmente tentará chamar zip em [3] e []. Chega-se então ao padrão da condição limite e assim o resultado é (1,'a'):(2,'b'):[], que é exatamente o mesmo que [(1,'a'),(2,'b')].

Vamos implementar mais uma função da biblioteca padrão — elem. Ela pega um elemento e uma lista e vê se aquele elemento está na lista. A condição limite, como na maioria das vezes com listas, é a lista vazia. Nós sabemos que uma lista vazia não contém elemento algum, então temos certeza que ela não tem o que estamos procurando.

elem' :: (Eq a) => a -> [a] -> Bool
elem' a [] = False
elem' a (x:xs)
    | a == x    = True
    | otherwise = a `elem'` xs

Bastante simples e previsível. Se a cabeça não é o elemento, então nós checamos a cauda. Se alcançarmos uma lista vazia, então o resultado é False.

Ordem, rápido!

Vamos supor que temos uma lista de itens que podem ser ordenados. Seu tipo é uma instância da typeclass Ord e agora queremos ordená-los! Existe um algoritmo muito legal para ordenação chamado quicksort. Que é uma maneira muito inteligente de ordenar itens. Para implementar ele em uma linguagem imperativa geralmente precisamos de 10 ou mais linhas, enquanto que em Haskell além de mais curta, será mais elegante. O quicksort se tornou um tipo de garoto propaganda do Haskell. Portanto, vamos implementá-lo, mesmo sabendo que fazer o quicksort em Haskell é considerado jogo sujo.

Então, a nossa declaração de tipo será quicksort :: (Ord a) => [a] -> [a]. Nada de novo. A condição limite? Lista vazia, como já esperado. Uma lista vazia ordenada é uma lista vazia. Agora vem o algoritmo principal: uma lista ordenada é uma lista composta de uma outra lista ordenada até um elemento X de valores menores que X, seguido de outra lista ordenada de valores maiores que X. Note que falamos de duas listas ordenadas, então provavelmente teremos que fazer uma chamada recursiva duas vezes! Note ainda que usamos o termo é para definir o algoritmo em vez de dizer faz isto, faz aquilo, então faz aquele outro.... Essa é a beleza da programação funcional! Mas como vamos filtrar a lista para somente obter elementos menores que a cabeça da nossa lista e somente elementos maiores que ela? Compreensão de listas. Vamos então definir logo de uma vez essa função.

quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
    let smallerSorted = quicksort [a | a <- xs, a <= x]
        biggerSorted = quicksort [a | a <- xs, a > x]
    in  smallerSorted ++ [x] ++ biggerSorted

Vamos fazer uma pequena rodada de testes para ver se ela está se comportando corretamente.

ghci> quicksort [10,2,5,3,1,6,7,4,2,3,4,8,9]
[1,2,2,3,3,4,4,5,6,7,8,9,10]
ghci> quicksort "a raposa pulou por cima do cachoro dorminhoco"
"       aaaaaccccddhhiilmmnoooooooooppprrrrsuu"

É isso ai! Era disso que eu tava falando! Então se a gente tiver algo como [5,1,9,4,6,7,3] e quiser ordenar isso, o algoritmo primeiro pegará o primeiro elemento que é 5 e colocará ele entre as listas de números menores e de números maiores. Assim, você passará a ter [1,4,3] ++ [5] ++ [9,6,7]. Nós sabemos que uma vez a lista esteja completamente ordenada, o número 5 ficará na quarta posição, já que há 3 números menores que ele e 3 números maiores que ele. Agora basta ordenarmos [1,4,3] e [9,6,7] para termos uma lista ordenada! Ordenamos as duas listas usando a mesma função. Eventualmente, quebraremos a lista tantas vezes que chegaremos a uma lista vazia que, pela nossa definição, já é uma lista ordenada. Aí vai uma ilustração:

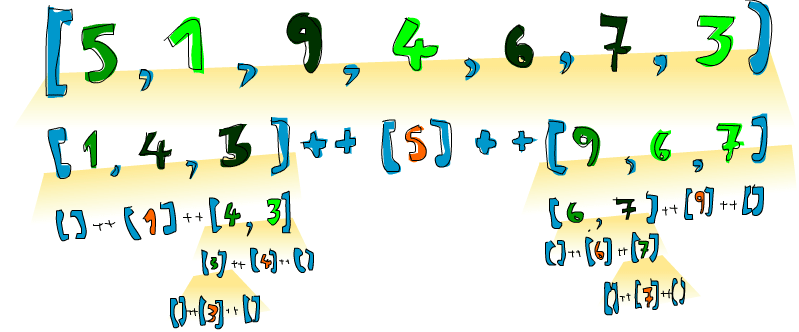
Um elemento que já encontrou seu lugar final é representado pela cor laranja. Se você lê-los da esquerda para a direita, verá a lista ordenada. Apesar de nós termos escolhido comparar todos os elementos com o primeiro, poderíamos ter usado qualquer outro elemento. No quicksort, o elemento que você irá comparar é chamado de pivô. Ele aqui esta em verde. Nós escolhemos o primeiro porque é mais fácil de pegar usando pattern matching. Os elementos que são menores que o pivô estão em verde claro e os elementos maiores que o pivô estão em verde escuro. E aquele negócio amarelo no meio de tudo representa a execução do quicksort.

Pensando recursivamente

Já fizemos alguma coisa de recursão até agora e, como você provavelmente já notou, existe um padrão aqui. Normalmente você define uma condição limite e então você define uma função que faz alguma coisa com o primeiro elemento e reaplica no resto. Não importa se é uma lista, uma árvore ou qualquer outra estrutura de dados. Uma soma é o primeiro elemento de uma lista mais a soma do resto da lista. O produto de uma lista é o primeiro elemento da lista multiplicado pelo produto do resto da lista. O tamanho de uma lista é primeiro elemento mais o tamanho do resto da lista. E por ai vai.

E claro, falamos também das condições limite. Normalmente o caso limite é um cenário onde uma aplicação recursiva não faz sentido. Quando se trata de listas, a condição limite é na maioria das vezes uma lista vazia. Se você está lidando com árvores, o caso limite é normalmente um nodo que não tem filho algum. Coitado...

Não é diferente quando estamos lidando com números recursivamente. Um número faz algum cálculo com alguma modificação dele. Quando fizemos a função de fatorial, era o número multiplicado pelo fatorial (dele - 1). Nesse caso, tal aplicação recursiva não fazia sentido com zero, já que fatoriais estão definidos somente para inteiros positivos. Frequentemente os valores das condições limite acabam sendo sua identidade. A identidade da multiplicação é 1 porque se você multiplicar algum número por 1, você recebe de volta ele mesmo. Também ao fazer somas de listas, definimos a soma de uma lista vazia como 0 e 0 é a identidade da adição. No quicksort, o caso limite é a lista vazia e a identidade é também a lista vazia, porque se você adicionar uma lista vazia a uma lista, você apenas recebe de volta a lista original.

Então quando você tentar pensar de forma recursiva para resolver um problema, tente pensar em quando a solução recursiva não se aplica e tente ver se você pode usar isso como uma condição limite. Pense sobre identidades, se você vai dividir em partes os parâmetros da função (por exemplo, listas são normalmente divididas em primeiro elemento e resto, através de pattern matching) e em que parte você usará chamadas recursivas.