Criando seus próprios tipos e typeclasses

Nos capítulos anteriores, vimos alguns tipos e typeclasses de Haskell. Neste capítulo, aprenderemos como criar nossos próprios e colocá-los para funcionar!

Introdução a tipos de dados algébricos

Até agora, vimos vários tipos de dados. Bool, Int, Char, Maybe, etc. Mas como criar nosso próprio? Bom, um jeito é usar a palavra-chave data para definir um tipo. Vamos ver como o tipo Bool é definido na biblioteca padrão.

data Bool = False | True

data significa que estamos definindo um novo tipo de dados. A parte anterior a = diz o tipo, que é Bool. As de depois são value constructors (construtores de valores). Elas especificam os diferentes valores que o tipo pode assumir. O | pode ser lido como ou (OR). Então você pode ler tudo como: o tipo Bool pode ter valores True ou False. Ambos, nome do tipo e contrutores de valores devem começar com letras maiúsculas.

Da mesma maneira, podemos imaginar o tipo Int sendo definido como:

data Int = -2147483648 | -2147483647 | ... | -1 | 0 | 1 | 2 | ... | 2147483647

Os primeiro e último construtores são os valores menores e maiores possíveis de Int. Não é definido exatamente assim, as reticências estão aí apenas com propósitos ilustrativos já que omitimos uma grande quantidade de números.

Agora, vamos pensar como podemos representar uma forma geométrica em Haskell. Um jeito é usar tuplas. Um círculo pode ser algo como (43.1, 55.0, 10.4) onde o primeiro e o segundo campos são as coordenadas do centro do círculo e o terceiro é o raio. Parece bom, mas também serve para representar qualquer vetor 3D ou algo do gênero. A melhor solução seria dizer qual é a forma, se um círculo ou retângulo. Aí:

data Shape = Circle Float Float Float | Rectangle Float Float Float Float 

E agora? Acho que gostei disso. O value constructor Circle tem três campos float. Então quando escrevemos um value constructor, nós podemos opcionalmente adicionar tipos que o nosso novo tipo conterá. Aqui, os dois primeiros campos são as coordenadas do centro, o terceiro é o raio. O value constructor Rectangle tem quatro campos que aceitam floats. Os dois primeiros são as coordenadas do ponto superior esquerdo e os outros dois coordenadas do inferior direito.

Mas quando falo campos, quero dizer parâmetros. Value constructors são basicamente funções que retornam um valor em um tipo de dados. Vejamos como estão declarados os tipos desses dois construtores.

ghci> :t Circle
Circle :: Float -> Float -> Float -> Shape
ghci> :t Rectangle
Rectangle :: Float -> Float -> Float -> Float -> Shape

Legal, então value constructors são funções como todo o resto. Quem imaginaria? Vamos fazer uma função que recebe uma forma geométrica e que retorna a sua superfície.

surface :: Shape -> Float
surface (Circle _ _ r) = pi * r ^ 2
surface (Rectangle x1 y1 x2 y2) = (abs $ x2 - x1) * (abs $ y2 - y1)

A primeira coisa digna de nota é a declaração de tipo. Ela nos diz que uma função recebe uma forma geométrica e retorna um float. Nós não poderíamos declarar o tipo como Circle -> Float porque Circle não é um tipo, Shape é. Assim como não podemos escrever uma função declarando o seu tipo como True -> Int. A próxima coisa que vemos aqui é que podemos usar pattern match em construtores. Nós já fizemos isso (várias vezes por sinal) ao testar patterns por [] ou False ou 5, com a diferença que não haviam tantos campos. Nós apenas escrevemos o construtor e associamos seus campos a nomes. Como estamos interessados no raio, os dois primeiros campos não são importantes, que nos dizem onde o círculo está.

ghci> surface $ Circle 10 20 10
314.15927
ghci> surface $ Rectangle 0 0 100 100
10000.0

Ei, funciona! Mas se tentarmos escrever Circle 10 20 5 no prompt, teremos um erro. Isso é devido ao Haskell não saber mostrar nosso tipo de dado como string (ainda). Lembre-se, quando tentamos mostrar um valor na tela, Haskell primeiro executa a função show para conseguir a versão em string do nosso valor e mostrar no terminal. Para fazer o nosso tipo Shape parte da typeclass Show nós o modificamos desse modo:

data Shape = Circle Float Float Float | Rectangle Float Float Float Float deriving (Show)

Não vamos ir muito a fundo com o uso do deriving por enquanto. Digamos que se adicionarmos deriving (Show) no fim da declaração de data, Haskell automaticamente fará esse tipo parte da typeclass Show. Logo, podemos fazer assim:

ghci> Circle 10 20 5
Circle 10.0 20.0 5.0
ghci> Rectangle 50 230 60 90
Rectangle 50.0 230.0 60.0 90.0

Value constructors são funções, então podemos mapear e aplicá-los parcialmente. Se quisermos ter uma lista de círculos com diferentes raios, podemos fazer assim.

ghci> map (Circle 10 20) [4,5,6,6]
[Circle 10.0 20.0 4.0,Circle 10.0 20.0 5.0,Circle 10.0 20.0 6.0,Circle 10.0 20.0 6.0]

Nosso tipo de dados está bom, mas poderia estar melhor. Vamos criar um tipo de dados intermediário que define um ponto em um espaço bidimensional e então deixar nossas formas geométricas mais fáceis de se entender.

data Point = Point Float Float deriving (Show)
data Shape = Circle Point Float | Rectangle Point Point deriving (Show)

Perceba que quando definimos um ponto, usamos o mesmo nome para o tipo de dados e o value constructor. Isso não tem nenhum funcionamento especial, mas é um padrão informal para quando o value constructor só pode assumir um valor. Agora que o Circle tem dois campos, um deles do tipo Point e outro Float. Isso torna as coisas mais claras. E o mesmo para o retângulo. Só temos que modificar a função surface para passar a refletir as mudanças.

surface :: Shape -> Float
surface (Circle _ r) = pi * r ^ 2
surface (Rectangle (Point x1 y1) (Point x2 y2)) = (abs $ x2 - x1) * (abs $ y2 - y1)

A única coisa que tivemos que mudar foram os patterns. A parte que se refere ao círculo permanece igual. No pattern do retângulo, nós usamos pattern matching aninhadamente para conseguir as medidas das linhas da figura. Se quiséssemos os próprios pontos por alguma razão, poderíamos ter usado as-patterns.

ghci> surface (Rectangle (Point 0 0) (Point 100 100))
10000.0
ghci> surface (Circle (Point 0 0) 24)
1809.5574

Que tal uma função que move uma figura? Recebe uma figura, o tanto a se mover no eixo x e no eixo y para retornar uma nova figura de mesmas dimensões, localizada em outra posição.

nudge :: Shape -> Float -> Float -> Shape
nudge (Circle (Point x y) r) a b = Circle (Point (x+a) (y+b)) r
nudge (Rectangle (Point x1 y1) (Point x2 y2)) a b = Rectangle (Point (x1+a) (y1+b)) (Point (x2+a) (y2+b))

Bastante simples. Nós somamos a quantidade de movimento à cada um dos pontos da figura.

ghci> nudge (Circle (Point 34 34) 10) 5 10
Circle (Point 39.0 44.0) 10.0

Se não quisermos mexer diretamente com pontos, podemos criar funções auxiliares que criam figuras de qualquer tamanho nas coordenadas zero e a partir daí movê-las.

baseCircle :: Float -> Shape
baseCircle r = Circle (Point 0 0) r

baseRect :: Float -> Float -> Shape
baseRect width height = Rectangle (Point 0 0) (Point width height)

ghci> nudge (baseRect 40 100) 60 23
Rectangle (Point 60.0 23.0) (Point 100.0 123.0)

Você pode, é claro, exportar os tipos de dados em seus módulos. Para isso, apenas escreva o tipo junto das funções que está exportando e, entre parênteses, especifique os tipos dos construtores que devem ser exportados, separados por vírgulas. Se quiser exportar todos os construtores de valores de um tipo, apenas escreva ...

Se queremos exportar as funções e tipos que definimos no módulo, podemos usar algo como isso:

Com o Shape(..), exportamos todos os construtores de valores de Shape, o que significa que quem importar nosso módulo poderá criar formas usando os construtores de valores Rectangle e Circle. É o mesmo que escrever Shape (Rectangle, Circle).

Poderíamos ainda optar por exportar nenhum dos construtores de valores de Shape, escrevendo Shape no código de exportação. Desse modo, quem importasse o nosso módulo poderia criar formas usando as funções auxiliares baseCircle e baseRect. Data.Map funciona assim. Você não pode criar um mapa usando Map.Map [(1,2),(3,4)] porque não exporta o construtor de valor. De qualquer maneira, pode usando funções auxiliares como Map.fromList. Lembre-se, construtores de valores nada mais são do que funções que recebem campos como parâmetros e retornam valores do mesmo tipo (como Shape) e seu retorno. Então quando decidimos não exportá-los, proibimos que alguém importando nosso módulo os use. Mas se outras funções não retornam um tipo, podemos usá-las para criar valores dos tipos de dados costumizados.

Não exportar os construtores de valores de tipos de dados os fazem mais abstratos, de modo que escondemos a sua implementação. Vale ressaltar que quem importar nosso módulo não pode usar pattern match em construtores de valores.

Sintaxe de registro

Certo, recebemos a tarefa de criar um tipo de dado que descreva uma pessoa. A informação que desejamos armazenar sobre a pessoa é: nome, sobrenome, idade, altura, número do telefone e sabor favorito de sorvete. Não sei você, mas isso é tudo que eu quero saber sobre uma pessoa. Vamos testar!

data Person = Person String String Int Float String String deriving (Show)

Certo. O primeiro campo é o nome, o segundo é o sobrenome, o terceiro é a idade e assim por diante. Vamos fazer uma pessoa.

ghci> let guy = Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate"
ghci> guy
Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate"

Até que é legal, entretanto levemente ilegível. E se nós quisermos criar uma função que consiga informação separada da pessoa? Uma função que nos dá o nome da pessoa, uma função que nos dá o sobrenome da pessoa, etc. Bem, teríamos que defini-las mais ou menos dessa forma.

firstName :: Person -> String
firstName (Person firstname _ _ _ _ _) = firstname

lastName :: Person -> String
lastName (Person _ lastname _ _ _ _) = lastname

age :: Person -> Int
age (Person _ _ age _ _ _) = age

height :: Person -> Float
height (Person _ _ _ height _ _) = height

phoneNumber :: Person -> String
phoneNumber (Person _ _ _ _ number _) = number

flavor :: Person -> String
flavor (Person _ _ _ _ _ flavor) = flavor

Vish! Eu certamente não curti escrever tudo isso! Apesar disso ser muito incomodo e ENTEDIANTE de se escrever, esse método funciona.

ghci> let guy = Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate"
ghci> firstName guy
"Buddy"
ghci> height guy
184.2
ghci> flavor guy
"Chocolate"

Deve existir um jeito melhor, você deve estar pensando! Bem, não, não há, desculpe.

Brincadeira, tem sim. Hahaha! Os criadores de Haskell eram muito espertos e anteciparam esse cenário. Eles incluíram uma forma alternativa de se escrever tipos de dados. Aqui está como nós poderíamos alcançar a funcionalidade mostrada acima utilizando sintaxe de registro.

data Person = Person { firstName :: String
                     , lastName :: String
                     , age :: Int
                     , height :: Float
                     , phoneNumber :: String
                     , flavor :: String
                     } deriving (Show) 

Então ao invés de apenas nomear os tipos de campos um após o outro e separá-los com espaços, nós utilizamos chaves. Primeiro escrevemos o nome do campo, por exemplo, firstName, depois escrevemos dois pontos duplos :: (também chamados de Paamayim Nekudotayim, haha) e então especificamos seu tipo. O tipo de dado resultante é exatamente o mesmo. O principal benefício disso é que se cria funções que consultam os campos no tipo de dado. Ao utilizar sintaxe de registro para criar esse tipo de dado, Haskell automaticamente criou essas funções: firstName, lastName, age, height, phoneNumber e flavor.

ghci> :t flavor
flavor :: Person -> String
ghci> :t firstName
firstName :: Person -> String

Ainda há outro benefício ao se utilizar sintaxe de registro. Quando derivamos Show para o tipo, ele se exibe diferentemente se utilizarmos sintaxe de registro para definir e instanciar o tipo. Digamos que nós temos um tipo que representa um carro. Queremos manter o registro da companhia que o fez, o nome do modelo e o ano de sua produção. Observe.

data Car = Car String String Int deriving (Show)

ghci> Car "Ford" "Mustang" 1967
Car "Ford" "Mustang" 1967

Se nós o definirmos utilizando sintaxe de registro, podemos fazer um novo carro dessa maneira.

data Car = Car {company :: String, model :: String, year :: Int} deriving (Show)

ghci> Car {company="Ford", model="Mustang", year=1967}
Car {company = "Ford", model = "Mustang", year = 1967}

Quando estamos fazendo um novo carro, não temos que necessariamente colocar os campos na ordem exata, contanto que listemos todos eles. Mas se não utilizarmos sintaxe de registro, temos de especificá-los em ordem.

Utilize sintaxe de registro quando um construtor tiver vários campos e não for óbvio o que cada campo tem. Se fizermos um tipo de dado de um vetor 3D escrevendo data Vector = Vector Int Int Int, é bem óbvio que os campos são componentes de um vetor. Entretanto, nos tipo de Person e Car, não era tão óbvio e nós nos beneficiamos muito do uso de sintaxe de registro.

Tipos paramétricos

Um construtor de valor pode pegar alguns parâmetros de valores e então produzir um novo valor. Por exemplo, o construtor Car pega três valores e produz um valor de carro. De maneira similar, construtores de tipo (type constructors) podem pegar tipos como parâmetros e produzir novos tipos. Isso pode parecer um pouco meta à primeira vista, mas não é muito complicado. Se você tem familiaridade com os templates de C++, você verá alguns pontos paralelos. Para se ter uma imagem clara de como os parâmetros de tipos funcionam na prática, vamos dar uma olhada em como um tipo que você já encontrou é implementado.

data Maybe a = Nothing | Just a

O a aqui é um parâmetro de tipo. E por haver um parâmetro de tipo envolvido, chamamos Maybe um construtor de tipo. Dependendo do que quisermos que esse tipo de dado guarde quando não for Nothing, esse construtor de tipo pode acabar produzindo um tipo Maybe Int, Maybe Car, Maybe String, etc. Nenhum valor pode ter um tipo de apenas Maybe, isso porque ele não é um tipo por si só, é um construtor de tipo. Para que isso se torne um tipo real do qual um valor pode ser parte, ele tem que ter todos os seus parâmetros preenchidos.

Então se passarmos Char como o parâmetro de tipo para Maybe, obtemos o tipo de Maybe Char. O valor Just 'a' tem um tipo de Maybe Char, por exemplo.

Você pode não saber disso, mas nós usamos um tipo que tem um parâmetro de tipo antes de usar Maybe. Estamos falando do tipo lista. Apesar de haver algum açúcar sintático na jogada, o tipo lista pega um parâmetro para produzir um tipo concreto. Valores podem ter um tipo [Int], um tipo [Char], um tipo [[String]], mas você não pode ter um valor que tenha um tipo de apenas [].

Vamos brincar um pouco com o tipo Maybe.

ghci> Just "Haha"
Just "Haha"
ghci> Just 84
Just 84
ghci> :t Just "Haha"
Just "Haha" :: Maybe [Char]
ghci> :t Just 84
Just 84 :: (Num t) => Maybe t
ghci> :t Nothing
Nothing :: Maybe a
ghci> Just 10 :: Maybe Double
Just 10.0

Parâmetros de tipo são úteis porque podemos criar diferentes tipos com eles dependendo de que espécie de tipos desejamos ter guardados no nosso tipo de dado. Quando fazemos :t Just "haha", o mecanismo de inferência de tipo descobre que isso é do tipo Maybe [Char], porque se o a no código Just a for uma String, entãp o a em Maybe a também deve ser uma String.

Perceba que o tipo de Nothing é Maybe a. Seu tipo é polimórfico. Se alguma função precisar de um Maybe Int como parâmetro, podemos passar um Nothing, porque Nothing não contém um valor, logo não importa. O tipo Maybe a pode agir como um Maybe Int se ele tiver de fazê-lo, assim como 5 pode agir como um Int ou um Double. Similarmente, o tipo da lista vazia é [a]. Uma lista vazia pode agir como um lista de qualquer coisa. Por isso que podemos fazer [1, 2, 3] ++ [] e [!ha", "ha", "ha"] ++ [].

Usar parâmetros de tipos é muito benéfico, mas apenas quando usá-los faz sentido. Geralmente nós usamos quando nossos tipos de dados pudessem funcionar, independentemente do tipo do valor que está guardado dentro de si, como no nosso tipo Maybe a. Se nosso tipo se comportar como uma espécie de caixa, isso será bom para o utilizarmos. Poderíamos mudar nosso tipo de dado Car assim:

data Car = Car { company :: String
               , model :: String
               , year :: Int
               } deriving (Show)

Para isso:

data Car a b c = Car { company :: a
                     , model :: b
                     , year :: c 
                     } deriving (Show)

Mas haveria algum benefício? A resposta é: provavelmente não, uma vez que acabaríamos apenas definindo funções que apenas funcionariam com o tipo Car String String Int. Por exemplo, dada nossa primeira definição de Car, poderíamos criar uma função que exibe as propriedades do carro em um texto pequeno e legal.

tellCar :: Car -> String
tellCar (Car {company = c, model = m, year = y}) = "This " ++ c ++ " " ++ m ++ " was made in " ++ show y

ghci> let stang = Car {company="Ford", model="Mustang", year=1967}
ghci> tellCar stang
"This Ford Mustang was made in 1967"

Uma função pequenina e fofinha! A declaração de tipo é fofa e funciona bem. E se Car fosse Car a b c?

tellCar :: (Show a) => Car String String a -> String
tellCar (Car {company = c, model = m, year = y}) = "This " ++ c ++ " " ++ m ++ " was made in " ++ show y

Teríamos de forçar essa função a usar o tipo de Car de (Show a) => Car String String a. Você pode ver que a assinatura de tipo é mais complicada e o único benefício que nós obteríamos seria que agora podemos usar qualquer tipo que seja uma instância da typeclass Show como o tipo para c.

ghci> tellCar (Car "Ford" "Mustang" 1967)
"This Ford Mustang was made in 1967"
ghci> tellCar (Car "Ford" "Mustang" "nineteen sixty seven")
"This Ford Mustang was made in \"nineteen sixty seven\""
ghci> :t Car "Ford" "Mustang" 1967
Car "Ford" "Mustang" 1967 :: (Num t) => Car [Char] [Char] t
ghci> :t Car "Ford" "Mustang" "nineteen sixty seven"
Car "Ford" "Mustang" "nineteen sixty seven" :: Car [Char] [Char] [Char]

Entretanto na vida real, nós acabaríamos usando Car String String Int na maioria das vezes e então pareceria que parametrizar o tipo Car não vale à pena. Nós geralmente utilizamos parâmetros de tipos quando o tipo que está contido dentro dos vários construtores de valor de tipos de dados não é realmente importante para o funcionamento do tipo. Uma lista de coisas é uma lista de coisas e não importa o tipo dessas coisas, a lista ainda funciona. Se quisermos somar uma lista de números, podemos especificar depois como a função de soma funciona especificamente para lista de números. O mesmo serve para Maybe. Maybe representa uma opção de tanto não se ter nada como se ter alguma coisa. Não importa o tipo dessa coisa.

Outro exemplo de um tipo parametrizado que já encontramos por aí é Map k v de Data.Map. O k é o tipo das chaves em um mapa e v é o tipo dos valores. Esse é um bom exemplo de onde os parâmetros são muito úteis. Ter mapas parametrizados nos permite ter mapeamentos de qualquer tipo para qualquer outro tipo, contanto que o tipo da chave seja parte da typeclass Ord. Se estivéssemos definindo um tipo mapeador, poderíamos adicionar uma restrição de typeclass na declaração data:

data (Ord k) => Map k v = ...

Entretanto, existe uma convenção muito forte em Haskell para nunca adicionar restrições de typeclass na declaração de dados. . Por quê? Bem, porque não há muitos benefícios, mas acabamos escrevendo mais restrições de classe, até quando não precisamos delas. Se colocarmos ou não a restriçãoOrd k na declaração data para Map k v, teríamos de colocar uma restrição nas funções que assumem que as chaves de um mapa podem ser ordenadas. Mas se não colocarmos a restrição na declaração do dado, não teremos de colocar Ord k na declaração de tipos de função que não se importam se k pode ser ordenado ou não. Um exemplo de tal função é toList, que apenas pega um mapeamento e converte-o em uma lista associativa. Sua assinatura de tipo é toList :: Map k a -> [(k, a)]. Se Map k v tivesse uma restrição de tipo na sua declaração data, o tpo para toList teria de ser toList :: (Ord k) => Map k a -> [(k, a)], mesmo que a função não fizesse nenhuma comparação de ordem entre as chaves.

Então não coloque restrições de tipo em declarações data mesmo se parecer fazer sentido, porque você terá de colocá-las nas declarações de função de qualquer forma.

Vamos implementar um tipo de vetor 3D e adicionar algumas operações para ele. Usaremos um tipo parametrizado porque mesmo sabendo que, em geral, o vetor conterá números, ainda vale a pena dar suporte a vários deles.

data Vector a = Vector a a a deriving (Show)

vplus :: (Num t) => Vector t -> Vector t -> Vector t
(Vector i j k) `vplus` (Vector l m n) = Vector (i+l) (j+m) (k+n)

vectMult :: (Num t) => Vector t -> t -> Vector t
(Vector i j k) `vectMult` m = Vector (i*m) (j*m) (k*m)

scalarMult :: (Num t) => Vector t -> Vector t -> t
(Vector i j k) `scalarMult` (Vector l m n) = i*l + j*m + k*n

vplus é para adicionar dois vetores. Dois vetores são adicionados apenas somando seus respectivos componentes.scalarMult é para o produto escalar entre dois vetores e vectMult é para multiplicar um vetor por um escalar. Essas funções podem operar nos tipos de Vector Int, Vector Integer, Vector Float, qualquer coisa, contanto que a de Vector a seja da typeclas Num. Além disso, se você examinar a declaração de tipo dessas funções, você verá que elas apenas podem operar em vetores do mesmo tipo e os números envolvidos devem ser do mesmo tipo que está contido dentro dos vetores. Perceba que não colocamos uma restrição de classe Num na declaração data, uma vez que teríamos que repeti-la nas funções de qualquer forma.

Mais uma vez, é importante distinguir entre o construtor de tipo e o construtor de valor. Quando estamos declarando um tipo de dado, a parte antes do = é o construtor de tipo e os construtores depois dele (possivelmente separados por |'s) são construtores de valor. Dar um tipo Vector t t t -> Vector t t t -> t à uma função seria errado porque temos que colocar os tipos na declaração de tipo e o construtor de tipo vetor recebe apenas um parâmetro, enquanto que o construtor de valor recebe três. Vamos brincar com nossos vetores.

ghci> Vector 3 5 8 `vplus` Vector 9 2 8
Vector 12 7 16
ghci> Vector 3 5 8 `vplus` Vector 9 2 8 `vplus` Vector 0 2 3
Vector 12 9 19
ghci> Vector 3 9 7 `vectMult` 10
Vector 30 90 70
ghci> Vector 4 9 5 `scalarMult` Vector 9.0 2.0 4.0
74.0
ghci> Vector 2 9 3 `vectMult` (Vector 4 9 5 `scalarMult` Vector 9 2 4)
Vector 148 666 222

Instâncias derivadas

Na sessão Basicão de Typeclasses, nós mostramos as bases das typeclasses. Nós mostramos que a typeclass é uma espécie de interface que define algum comportamento. Um tipo pode criar uma instância de uma typeclass se ele suportar esse comportamento. Exemplo: o tipo Int é uma instância da typeclass Eq pois a typeclass Eq define o comportamento de coisas que podem ser comparadas. E como inteiros podem ser comparados, Int é parte da typeclass Eq. A real utilidade vêm com funções que agem como uma interface para Eq, chamada == e /=. Se um tipo é parte da typeclass Eq, nós podemos usar a função == com valores desse tipo. Esse é porque expressões como 4 == 4 e "foo" /= "bar" tem os tipos checados.

Nós também mencionamos que eles são geralmente confundidos com classes em linguagens como Java, Python, C++ e similares, o que confunde muitas pessoas. Nessas linguagens, classes são como um modelo pelo qual nós criamos objetos que contém estado e pode realizar algumas ações. Typeclasses são mais como interfaces. Nós não construímos dados a partir de typeclasses. Em vez disso, primeiro construímos nosso tipo de dado e então nós pensamos como ele pode agir. Se ele pode agir como algo que pode ser comparado, nós fazemos dele uma instância da typeclass Eq. Se ele pode agir como algo que pode ser ordenado, nós fazemos dele uma instância da typeclass Ord.

Na próxima sessão, vamos dar uma olhada como podemos manualmente fazer nossas instâncias de tipos de uma typeclass implementando funções definidas pela typeclass. Mas por enquanto vamos ver como Haskell pode automaticamente fazer do nosso tipo uma instância de alguma das seguintes typeclasses: Eq, Ord, Enum, Bounded, Show, Read. Haskell pode derivar o comportamento dos nossos tipos nesse contexto se nós usarmos a palavra reservada deriving quando construímos o nosso tipo.

Considere este tipo de dados:

data Person = Person { firstName :: String
                     , lastName :: String
                     , age :: Int
                     }

Ele descreve uma pessoa. Vamos assumir que não existe duas pessoas com a mesma combinação de primeiro nome, sobrenome e idade. Agora, se nós temos registros de duas pessoas, faz algum sentido ver se eles representam a mesma pessoa? Sim, faz. Nós podemos tentar comparar ambas e ver que elas são ou não iguais. É por isso que não faz sentido para esse tipo fazer parte da Eq. Nós vamos derivar a instância.

data Person = Person { firstName :: String
                     , lastName :: String
                     , age :: Int
                     } deriving (Eq)

Quando nós derivamos uma instância de Eq para um tipo e tentamos comparar os dois valores desse tipos com == ou /=, Haskell verá se o valor dos construtores são correspondentes (há apenas um único construtor cujo valor passa) e então ele irá checar se todos os dados internos correspondem testando cada par de campos com ==. Há apenas um problema, os tipos de todos os campos também tem de fazer parte da typeclass Eq. Mas uma vez que ambos são String e Int, então OK. Vamos testar nossa instância de Eq.

ghci> let mikeD = Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> let adRock = Person {firstName = "Adam", lastName = "Horovitz", age = 41}
ghci> let mca = Person {firstName = "Adam", lastName = "Yauch", age = 44}
ghci> mca == adRock
False
ghci> mikeD == adRock
False
ghci> mikeD == mikeD
True
ghci> mikeD == Person {firstName = "Michael", lastName = "Diamond", age = 43}
True

Claro, uma vez que Person agora está em Eq, nós podemos usá-lo como a para todas as funções que tem a restrição de class para Eq a em sua assinatura, como elem.

ghci> let beastieBoys = [mca, adRock, mikeD]
ghci> mikeD `elem` beastieBoys
True

As typeclasses Show e Read são para coisas que podem ser convertidas de e para strings, respectivamente. Assim como Eq, se o construtor de um tipo tiver campos, seu tipo precisa fazer parte de Show ou Read se nós quisermos fazer do nosso tipo uma instância deles. Vamos fazer nosso tipo de dados Person também fazer parte de Show e Read.

data Person = Person { firstName :: String
                     , lastName :: String
                     , age :: Int
                     } deriving (Eq, Show, Read)

Agora nós podemos imprimir uma pessoa no terminal.

ghci> let mikeD = Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> mikeD
Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> "mikeD is: " ++ show mikeD
"mikeD is: Person {firstName = \"Michael\", lastName = \"Diamond\", age = 43}"

Se nós tentássemos imprimir uma pessoa no terminal antes de tornar o tipo Person parte de Show, Haskell teria reclamado para nós, afirmando que ele não sabia como representar uma pessoa como uma string. Mas agora que nós derivamos uma instância de Show para ela, ele saberá como.

Read é praticamente a typeclass inversa à Show. Show é para conversão de valores de um tipo em uma string, Read é para conversão de strings para valores de um tipo. Lembre-se, quando nós usamos a função read, nós temos que usar uma notação de tipo explicita para dizer ao Haskell qual o tipo que nós queremos pegar como resultado. Se nós não explicitamos o tipo que queremos como resultado, Haskell não vai saber que tipo nós queremos.

ghci> read "Person {firstName =\"Michael\", lastName =\"Diamond\", age = 43}" :: Person
Person {firstName = "Michael", lastName = "Diamond", age = 43}

Se usarmos depois o resultado do read de um jeito que Haskell possa inferir que isto deve ser uma pessoa, nós não temos que usar nenhuma notação de tipo.

ghci> read "Person {firstName =\"Michael\", lastName =\"Diamond\", age = 43}" == mikeD
True

Também podemos ler tipos parametrizados, mas nós temos que preencher os tipos dos parâmetros. Então não podemos fazer read "Just 't'" :: Maybe a, porém podemos fazer read "Just 't'" :: Maybe Char.

Instâncias derivadas de Ord agem como o esperado. Primeiro os construtores são comparados lexicograficamente e se o valor dos dois construtores forem os mesmos, seus campos são comparados, admitindo que os tipos dos seus campos também são instâncias de Ord. O tipo Bool pode ter o valor tanto de False ou True. Com a finalidade de ver como ele se comporta quando comparado, nós podemos pensar que ele é implementado da seguinte forma:

data Bool = False | True deriving (Ord)

Por causa do construtor de valor False ser especificado primeiro e o construtor de valor True ser especificado logo em seguida, nós podemos considerar True como maior que False.

ghci> True `compare` False
GT
ghci> True > False
True
ghci> True < False
False

No tipo Maybe a, o construtor de valor Nothing é especificado antes do construtor de valor Just, portanto o valor de Nothing é sempre menor que o valor de Just algumacoisa, mesmo que algumacoisa seja menos um bilhão de trilhões. Mas se nós compararmos dois valores Just, então será comparado com o que há dentro deles.

ghci> Nothing < Just 100
True
ghci> Nothing > Just (-49999)
False
ghci> Just 3 `compare` Just 2
GT
ghci> Just 100 > Just 50
True

Mas nós não podemos fazer algo como Just (*3) > Just (*2), porque (*3) e (*2) são funções que não são instâncias de Ord.

Nós podemos facilmente usar tipos algébricos para fazer enumerações e as typeclasses Enum e Bounded nos ajudam com isso. Considere o seguinte tipo de dado:

data Day = Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday

Por causa de todos os valores de construtores serem nulos (não pegam parâmetros, ou seja, campos), nós podemos fazer com que sejam parte da typeclass Enum. A typeclass Enum é para coisas que tem predecessor e sucessor. Nós podemos faze-los também parte da typeclass Bounded, que é para coisas que tem um menor e um maior valor possível. E enquanto estamos no assunto, vamos torná-lo uma instância de todos as outras typeclasses derivadas e ver o que podemos fazer com ele.

data Day = Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday 
           deriving (Eq, Ord, Show, Read, Bounded, Enum)

Por ele ser parte das typeclasses Show e Read, nós podemos converter os valores desse tipo, de e para strings.

ghci> Wednesday
Wednesday
ghci> show Wednesday
"Wednesday"
ghci> read "Saturday" :: Day
Saturday

Por ele ser parte das typeclasses Eq e Ord, nós podemos comparar ou equiparar dias.

ghci> Saturday == Sunday
False
ghci> Saturday == Saturday
True
ghci> Saturday > Friday
True
ghci> Monday `compare` Wednesday
LT

Ele também é parte de Bounded, portanto nós podemos pegar o menor e o maior dia.

ghci> minBound :: Day
Monday
ghci> maxBound :: Day
Sunday

Ele também é uma instância de Enum. Nós podemos pegar os predecessores e sucessores dos dias e fazer listas de intervalos com eles.

ghci> succ Monday
Tuesday
ghci> pred Saturday
Friday
ghci> [Thursday .. Sunday]
[Thursday,Friday,Saturday,Sunday]
ghci> [minBound .. maxBound] :: [Day]
[Monday,Tuesday,Wednesday,Thursday,Friday,Saturday,Sunday]

Isso é bem impressionante.

Tipos sinônimos

Anteriormente, mencionamos que quando escrevemos tipos, os tipos [Char] e String são equivalentes e substituíveis. Isso é implementado com tipos sinônimos . Tipos sinônimos na verdade não fazem nada por si só, eles são apenas um jeito de dar nomes diferentes para alguns tipos fazerem mais sentido quando alguém estiver lendo o nosso código e a documentação. Veja como a biblioteca padrão define String como um sinônimo para [Char].

 type String = [Char]
 

Nós já fomos apresentados a palavra reservada type. A palavra reservada pode ser confusa para alguns, pois não estamos fazendo nada de novo (nós já fizemos isso com a palavra reservada data), mas apenas estamos criando um sinônimo para um tipo que já existente.

Se criarmos uma função que converte uma string para CAIXA ALTA e chamá-la de toUpperString ou qualquer outro nome, podemos dar a ela uma declaração do tipo toUpperString :: [Char] -> [Char] ou toUpperString :: String -> String. Ambas são essencialmente a mesma coisa, com a diferença de que a última é bem mais agradável de se ler.

Quando estávamos mexendo com o módulo Data.Map, nós primeiro representamos uma agenda como sendo uma lista de associações antes de converte-la em um mapeamento. Como já descobrimos antes, uma lista de associações é uma lista com pares de chaves-valores. Vamos dar uma olhada na nossa agenda (phoneBook).

phoneBook :: [(String,String)]
phoneBook =    
    [("betty","555-2938")   
    ,("bonnie","452-2928")   
    ,("patsy","493-2928")   
    ,("lucille","205-2928")   
    ,("wendy","939-8282")   
    ,("penny","853-2492")   
    ]

Nós vimos que o tipo de phoneBook é [(String,String)]. Isso nos diz que ela é uma lista de associações que mapeia de uma string para outra string, só isso. Vamos criar um tipo sinônimo que transmita alguma informação a mais na declaração do tipo.

type PhoneBook = [(String,String)]

Agora a declaração de tipo para nossa agenda pode ser feita como phoneBook :: PhoneBook. Vamos fazer também um tipo sinônimo para String.

type PhoneNumber = String
type Name = String
type PhoneBook = [(Name,PhoneNumber)]

Dar um tipo sinônimo a String é algo que um programador Haskell faz quando ele quer transmitir mais informação sobre como a string pode ser usada em sua função e o que ela representa.

Então, quando implementarmos agora uma função que pega um nome e um número e soubermos que essa combinação de nome e número está em nossa agenda (PhoneBook), vamos poder dar uma declaração muito mais bonita e descritiva sobre o tipo.

inPhoneBook :: Name -> PhoneNumber -> PhoneBook -> Bool
inPhoneBook name pnumber pbook = (name,pnumber) `elem` pbook

Se nós decidirmos não usar tipos sinônimos, nossas funções podem ter um tipo como String -> String -> [(String,String)] -> Bool. Neste caso, a declaração de tipo que aproveita o uso de tipos sinônimos é mais fácil de entender. Entretanto, você não pode fazer tudo com eles. Nós introduzimos tipos sinônimos ou para descrever o que algum tipo existente representa em nossas funções (e assim nossas declarações de tipos se tornam mais bem documentadas) ou quando algum tipo é grande demais para ser repetido várias vezes (como [(String,String)]) mas representa algo mais específico no contexto das nossas funções.

Tipos sinônimos podem ser parametrizados. Se nós quisermos que um tipo represente uma lista de associação de tipos mas permaneça genérico o suficiente para ser usado com qualquer tipo de chaves e valores, nós podemos fazer isso:

type AssocList k v = [(k,v)]

Agora, a função que obtêm o valor de uma chave na lista de associações pode ter o seguinte tipo (Eq k) => k -> AssocList k v -> Maybe v. O tipo AssocList é um construtor que pega dois tipos e produz um tipo concreto, como AssocList Int String, por exemplo.

Assim como podemos aplicar parcialmente funções para pegar novas funções, nós podemos aplicar parcialmente tipos paramétricos e pegar novos construtores de tipo a partir deles. Assim como chamamos uma função com poucos parâmetros e pegamos uma nova função como retorno, nós podemos também especificar um construtor de tipos com poucos parâmetros e pegar de volta um construtor de tipo aplicado parcialmente. Se nós queremos um tipos que represente um mapeamento (de Data.Map) de inteiros para alguma coisa, nós podemos então fazer isto:

type IntMap v = Map Int v

Ou nós podemos fazer algo como isto:

type IntMap = Map Int

De qualquer forma, o código do construtor de tipos IntMap pega um parâmetro e esse será o tipo ao qual os inteiros irão apontar.

Tenha certeza de que você realmente entendeu a diferença entre construtores de tipos e construtores de valores. Só porque nós fizemos um tipo sinônimo chamado IntMap ou AssocList não significa que nós podemos fazer coisas como AssocList [(1,2),(4,5),(7,9)]. Tudo isso significa que nós podemos nos referir a esse tipo usando diferentes nomes. Nós podemos fazer [(1,2),(3,5),(8,9)] :: AssocList Int Int, que irá fazer os números dentro dela assumir o tipo de Int, mas nós podemos ainda continuar usando essa lista como faríamos com qualquer lista normal que tem pares de inteiros dentro dela. Tipos sinônimos (e tipos em geral) somente podem ser usados na porção de tipos do Haskell. Nós estamos na porção de tipos do Haskell sempre quando definimos novos tipos (como na declaração de data e type) ou quando estamos após um ::. O :: esta em declarações de tipos ou em anotações de tipos.

Outro tipo interessante de dados que recebe dois tipos como parâmetros é o tipo Either a b. É assim que ele é mais ou menos definido:

data Either a b = Left a | Right b deriving (Eq, Ord, Read, Show)

Há dois construtores de valores. Se Left for usado, então o seu conteúdo é do tipo a e se Right for usado, então o seu conteúdo é do tipo b. Podemos então usar esse tipo para encapsular o valor de um tipo no outro e então quando temos um valor do tipo Either a b, nós normalmente vamos verificar o padrão de correspondência entre Left e Right e diferenciar as coisas com base no que eles eram.

ghci> Right 20
Right 20
ghci> Left "w00t"
Left "w00t"
ghci> :t Right 'a'
Right 'a' :: Either a Char
ghci> :t Left True
Left True :: Either Bool b

Até agora, vimos que Maybe a foi usado principalmente para representar os resultados de computações que poderiam ter falhado ou não. Mas algumas vezes, Maybe a não é bom o suficiente porque Nothing não transmite informação suficientemente boa de que algo falhou. Isso é legal para as funções que podem falhar de forma única ou se nós apenas estamos interessados em como e porque ela falhou. Um Data.Map falha ao pesquisar apenas se a chave que estávamos procurando não estava no mapa, então sabemos exatamente o que aconteceu. Entretanto, quando nós estamos interessados em como alguma função falhou e o porque, nós normalmente usamos o resultado do tipo Either a b, onde a é uma espécie de tipo que pode nos dizer algo sobre um possível erro e b é o tipo de uma computação realizada com sucesso. Portanto, erros usam o construtor de valor Left enquanto os resultados usam Right.

Um exemplo: uma escola de ensino médio tem armários para que os estudantes tenham algum lugar para pôr os seus pôsteres do Guns'n'Roses. Cada armário tem uma combinação de código. Quando um estudante quer um novo armário, ele irá falar para o supervisor dos armários o número do armário que ele quer e então o supervisor lhe dará um código. Entretanto, se alguém já estiver usando o armário, ele não poderá dizer o código do armário e terá que pegar um diferente. Nós iremos usar um mapa a partir de Data.Map para representar os armários. Ele vai mapear a partir dos números dos armários para um par de armários que estão em uso ou não e os códigos dos armários.

import qualified Data.Map as Map

data LockerState = Taken | Free deriving (Show, Eq)

type Code = String

type LockerMap = Map.Map Int (LockerState, Code)

Coisa simples. Nós introduzimos um novo tipo de dados para representar se um armário está ocupado ou livre e nós criamos um tipo sinônimo para o código do armário. Nós também criamos um tipo sinônimo para mapear pares de inteiros com o estado do armário e o seu código. E agora, vamos criar uma função que busca por um código no nosso mapa de armários. Vamos usar o tipo Either String Code para representar o nosso resultado, porque a nossa busca pode falhar de duas formas — o armário pode estar ocupado, neste caso nós não podemos dizer o código ou o número do armário pode nunca ter existido. Se a busca falhar, nós iremos usar uma String que nos dirá o que aconteceu.

lockerLookup :: Int -> LockerMap -> Either String Code
lockerLookup lockerNumber map = 
    case Map.lookup lockerNumber map of 
        Nothing -> Left $ "Locker number " ++ show lockerNumber ++ " doesn't exist!"
        Just (state, code) -> if state /= Taken 
                                then Right code
                                else Left $ "Locker " ++ show lockerNumber ++ " is already taken!"

Fizemos uma busca normal no mapa. Se nós recebemos um Nothing, vamos retornar um valor do tipo Left String, dizendo que o armário não existe. Se encontramos ele, então vamos fazer uma checagem adicional para ver se o armário já está ocupado. Se ele estiver, retornamos um Left dizendo que ele já está ocupado. Se não estiver ocupado, retornamos um valor do tipo Right Code, onde nós damos ao estudante o código correto do armário. Atualmente isto é um Right String, mas nós introduzimos aquele tipo sinônimo apenas como uma documentação adicional dentro da declaração do tipo. Aqui está um exemplo de mapeamento:

lockers :: LockerMap
lockers = Map.fromList 
    [(100,(Taken,"ZD39I"))
    ,(101,(Free,"JAH3I"))
    ,(103,(Free,"IQSA9"))
    ,(105,(Free,"QOTSA"))
    ,(109,(Taken,"893JJ"))
    ,(110,(Taken,"99292"))
    ]

Agora vamos tentar buscar alguns códigos de armários.

ghci> lockerLookup 101 lockers
Right "JAH3I"
ghci> lockerLookup 100 lockers
Left "Locker 100 is already taken!"
ghci> lockerLookup 102 lockers
Left "Locker number 102 doesn't exist!"
ghci> lockerLookup 110 lockers
Left "Locker 110 is already taken!"
ghci> lockerLookup 105 lockers
Right "QOTSA"

Nós podiamos ter usado um Maybe a para representar o resultado, mas nós não iriamos saber o porque de não podermos receber o código. Mas agora, nós temos informação sobre a falha no nosso tipo de resultado.

Estruturas de dados recursivas

Como nós vimos, um construtor em um tipo de dados algébrico pode ter muitos (ou nenhum) campos e cada um pode ser de algum tipo concreto. Com isso em mente, nós podemos fazer construtores cujo tipo dos campos são do mesmo tipo! Usando isso, nós podemos criar tipos de dados recursivos, onde o valor de um tipo contém valores daquele tipo, que por sua vez contém mais valores do mesmo tipo, e assim por diante.

Pense na lista: [5]. Isso é apenas açúcar sintático para 5:[]. Do lado esquerdo do :, há um valor e do lado direito, há uma lista. E neste caso, há uma lista vazia. E agora sobre a lista [4,5]? Bem, isso é desaçucarado para 4:(5:[]). Olhando para o primeiro :, nós vemos que isso também tem um elemento do lado esquerdo e uma lista (5:[]) do lado direito. O mesmo vale para uma lista como 3:4:5:6:[] (pois : é associativo a direita) ou [3,4,5,6].

Nós podemos dizer que a lista pode ser uma lista vazia ou ela pode ser um elemento unido com um : com outra lista (que pode ser outra lista vazia ou não).

Então vamos usar tipos de dados algébricos para implementar nossa própria lista!

data List a = Empty | Cons a (List a) deriving (Show, Read, Eq, Ord)

A leitura é quase como a da nossa definição de lista de um dos parágrafos anteriores. Isto é ou uma lista vazia ou a combinação de uma cabeça com algum valor e uma lista. Se você está confuso sobre isso, você pode achar mais fácil de entender a sintaxe dos registros.

data List a = Empty | Cons { listHead :: a, listTail :: List a} deriving (Show, Read, Eq, Ord)

Você também pode estar confuso com este construtor aqui Cons. cons é outra palavra para :. Você vê, em listas, : é atualmente um construtor que pega dois valores e outra lista e retorna uma lista. Nós já podemos usar o nosso novo tipo de lista! Em outras palavras, isto tem dois campos. Um campo é do tipo de a e o outro é do tipo de [a].

ghci> Empty
Empty
ghci> 5 `Cons` Empty
Cons 5 Empty
ghci> 4 `Cons` (5 `Cons` Empty)
Cons 4 (Cons 5 Empty)
ghci> 3 `Cons` (4 `Cons` (5 `Cons` Empty))
Cons 3 (Cons 4 (Cons 5 Empty))

Nós chamamos nosso construtor Cons de uma maneira infixada então você pode ver que ele é como :. Empty é como [] e 4 `Cons` (5 `Cons` Empty) é como 4:(5:[]).

Nós podemos definir funções para serem infixadas automaticamente, tornando-as compostas apenas por caracteres especiais. Nós também podemos fazer o mesmo com construtores, já que eles são apenas funções que retornam um tipo de dados. Veja isso então.

infixr 5 :-:
data List a = Empty | a :-: (List a) deriving (Show, Read, Eq, Ord)

Primeiramente, nós notamos uma nova construção sintática, as declarações de precedência. Quando nós definimos funções como operadores, nós podemos usar isso para dar uma precedência (mas não precisamos). Um estado de precedência é como hermeticamente associar um operador para ser ou associativo a esquerda ou associativo a direita. Por exemplo, * tem forma de precedência infixl 7 * e + tem forma de precedência infixl 6. Isto significa que eles são ambos associativos a esquerda (4 * 3 * 2 é (4 * 3) * 2) mas * associa mais que +, porque ele tem uma precedência maior, então 5 * 4 + 3 é (5 * 4) + 3.

Por outro lado, nós apenas escrevemos a :-: (List a) em vez de Cons a (List a). Agora nós podemos escrever as listas em nosso tipo de lista assim:

ghci> 3 :-: 4 :-: 5 :-: Empty
(:-:) 3 ((:-:) 4 ((:-:) 5 Empty))
ghci> let a = 3 :-: 4 :-: 5 :-: Empty
ghci> 100 :-: a
(:-:) 100 ((:-:) 3 ((:-:) 4 ((:-:) 5 Empty)))

Quando nossos tipos derivam de Show, Haskell permanecerá mostrando ele como se o construtor estivesse na forma de função prefixada, portanto com parênteses em volta do operador (lembre-se, 4 + 3 é (+) 4 3).

Vamos criar uma função que junta duas das nossas listas em uma. Assim é como ++ é definida para listas normais:

infixr 5  ++
(++) :: [a] -> [a] -> [a]
[]     ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys)

Então nós vamos apenas roubar para nossa própria lista. Nós iremos chamar a função de .++.

infixr 5  .++
(.++) :: List a -> List a -> List a 
Empty .++ ys = ys
(x :-: xs) .++ ys = x :-: (xs .++ ys)

E vamos ver se isso funciona ...

ghci> let a = 3 :-: 4 :-: 5 :-: Empty
ghci> let b = 6 :-: 7 :-: Empty
ghci> a .++ b
(:-:) 3 ((:-:) 4 ((:-:) 5 ((:-:) 6 ((:-:) 7 Empty))))

Legal. Isto é legal. Se nós quisermos, nós podemos implementar todas as funções que operam com listas usando nosso próprio tipo de lista.

Note como o padrão casa com (x :-: xs). Isso funciona porque o casamento de padrão é atualmente um casamento de construtores. Nós podemos casar com :-: porque ele é um construtor para o nosso tipo de lista e nós também podemos casar com : porque ele é um construtor para o tipo de lista padrão. O mesmo ocorre com []. Porque o casamento de padrão funciona (apenas) em construtores, nós podemos também casar para coisas como, construtores normalmente prefixados ou coisas como 8 ou 'a', que são basicamente construtores para tipos números e caracteres, respectivamente.

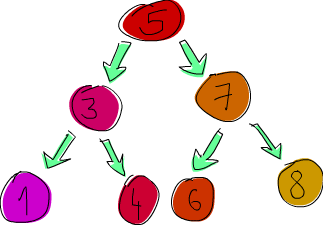
Agora, nós iremos implementar uma árvore de busca binária. Se você não esta familiarizado com árvores de busca binárias em linguagens como C, aqui está o que elas são: um elemento aponta para dois elementos, um deles está a esquerda e o outro a direita. O elemento da esquerda é menor, o elemento da direita é maior. Cada um destes elementos pode também apontar para dois elementos (ou um, ou nenhum). Na realidade, cada elemento tem até duas sub-árvores. A coisas legal sobre árvores de busca binária é que nós conhecemos que todos os elementos da sub-árvore esquerda são menores, dizendo, 5 tem de ser menor que 5. Elementos da sub-árvore direita serão maiores. Então se nós precisamos buscar por 8 em nossa árvore, nós começamos com 5 e então pelo fato de 8 ser maior que 5, nós iremos para a direita. Nós estamos agora no 7 e porque 8 é maior que 7, nós vamos para a direita novamente. E nós então encontramos nosso elemento em três etapas! Agora se isto for uma lista normal (ou uma árvore, mas não balanceada), podem ser necessários sete etapas em vez de três para ver se o 8 está lá.

Conjuntos e mapeamentos de Data.Set e Data.Map são implementados usando árvores, em vez de árvores de busca binária normais, eles usam árvores de busca binária balanceadas, que estão sempre balanceadas. Mas por enquanto, nós iremos apenas implementar uma árvore de busca binária normal.

Aqui está o que nós iremos dizer: uma árvore é ou uma árvore vazia ou é um elemento que contém algum valor e duas árvores. Soa perfeitamente bem para um tipo de dados algébrico!

data Tree a = EmptyTree | Node a (Tree a) (Tree a) deriving (Show, Read, Eq)

Ok, tudo bem, isso é bom. Em vez de manualmente construir uma árvore, nós iremos criar uma função que pega uma árvore e um elemento e insere um elemento nela. Nós fazemos isso pela comparação do valor que nós queremos inserir com o nó raiz e então se ele é menor, nós iremos para a esquerda, se ele é maior, nós iremos para direita. Nós fazemos o mesmo para cada nó subsequente até encontrar uma árvore vazia. Uma vez que nós encontramos uma árvore vazia, nós apenas inserimos um nó com o valor em vez de uma árvore vazia.

Em linguagens como C, nós fazemos isso pela modificação de ponteiros e valores dentro da árvore. Em Haskell, nós não podemos realmente modificar nossa árvore, então nós temos de fazer uma nova sub-árvore cada vez que nós decidimos ir para esquerda ou direita e no fim da função de inserção nós retornamos uma árvore completamente nova, porque Haskell realmente não tem um conceito de ponteiros, apenas valores. Por isso, o tipo de nossa função de inserção é algo como a -> Tree a - > Tree a. Ela pega um elemento e uma árvore e retorna uma nova árvore que tem o elemento inserido. Isto pode parecer como algo ineficiente, mas a avaliação preguiçosa cuida do problema.

Então, aqui há duas funções. Uma é uma função utilitária para fazer uma árvore monódica (uma árvore com apenas um nó) e uma função que insere um elemento na árvore.

singleton :: a -> Tree a
singleton x = Node x EmptyTree EmptyTree

treeInsert :: (Ord a) => a -> Tree a -> Tree a
treeInsert x EmptyTree = singleton x
treeInsert x (Node a left right) 
    | x == a = Node x left right
    | x < a  = Node a (treeInsert x left) right
    | x > a  = Node a left (treeInsert x right)

A função singleton é apenas um atalho para fazer um nó que tem alguma coisa e então duas sub-árvores vazias. Em nossa função de inserção, nós primeiro temos uma condição de limites como padrão. Se alcançarmos uma sub-árvore vazia, isso significa que nós estamos onde queremos e em vez de uma árvore vazia, nós pomos uma árvore monódica com nosso elemento. Se nós não estamos inserindo em uma árvore vazia, então nós temos de checar algumas coisas. Primeiro, se o elemento que nós estamos inserindo é igual ao elemento da raiz, apenas retornamos uma árvore que é ela mesma. Se ele é menor, retornamos uma árvore que tem o mesmo valor na raiz, a mesma sub-árvore a direita, mas em vez de sua sub-árvore esquerda, nós pomos uma árvore que tem nosso valor inserido nela. Da mesma forma (mas de forma contrária) fazemos isso se o elemento é maior que o elemento da raiz.

Em seguida, nós iremos criar uma função que checa se algum elemento está na árvore. Primeiro, vamos definir uma condição de limite. Se nós estamos buscando por um elemento em uma árvore vazia, então é certo que ele não está ali. Ok. Note como isto é o mesmo que uma condição de limites quando buscamos por um elemento em listas. Se nós estamos procurando por um elemento e uma lista vazia, ele não está lá. De qualquer maneira, se nós estamos procurando por um elemento em uma árvore que não está vazia, então nós checamos algumas coisas. Se o elemento na raiz do nó é o que nós estamos procurando, maravilha! Se não é, o que fazer então? Bem, nós podemos tirar vantagem do conhecimento de que todos os elementos a esquerda são menores que a raiz do nó. Então se o elemento que nós estamos procurando é menor que a raiz do nó, checamos para ver se ele está na sub-árvore esquerda. Se ele é maior, checamos para ver se ele não está na sub-árvore direita.

treeElem :: (Ord a) => a -> Tree a -> Bool
treeElem x EmptyTree = False
treeElem x (Node a left right)
    | x == a = True
    | x < a  = treeElem x left
    | x > a  = treeElem x right

Tudo o que tínhamos que fazer era escrever o parágrafo anterior em código. Vamos ter alguma diversão com nossas árvores! Em vez de manualmente construir uma (embora podemos), nós iremos usar um varredor de listas para construir uma árvore a partir de uma lista. Lembre-se, praticamente tudo que atravessa uma lista elemento por elemento e então retorna algum tipo de valor pode ser implementado com um interador de lista (fold)! Nós vamos iniciar com uma árvore vazia e então percorrer a lista da direita elemento por elemento inserindo-os na nossa árvore acumuladora.

ghci> let nums = [8,6,4,1,7,3,5]
ghci> let numsTree = foldr treeInsert EmptyTree nums
ghci> numsTree
Node 5 (Node 3 (Node 1 EmptyTree EmptyTree) (Node 4 EmptyTree EmptyTree)) (Node 7 (Node 6 EmptyTree EmptyTree) (Node 8 EmptyTree EmptyTree))

Nesse foldr, treeInsert foi uma função de interação (ela pega uma árvore e uma lista de elementos e produz uma nova árvore) e EmptyTree foi o acumulador inicial. nums, claro, foi a lista sobre a qual interamos.

Quando nós imprimimos nossa árvore no terminal, ela não é muito legível, mas se nós tentarmos, nós podemos decifrar esta estrutura. Nós vemos que o nó raiz é 5 e então há duas sub-árvores, uma que tem o nó raiz 3 e a outra um 7, e etc.

ghci> 8 `treeElem` numsTree
True
ghci> 100 `treeElem` numsTree
False
ghci> 1 `treeElem` numsTree
True
ghci> 10 `treeElem` numsTree
False

Verificar se um elemento pertence também funciona perfeitamente. Legal!

Então como você pode ver, estrutura de dados algébricos são um conceito realmente legal e poderosos em Haskell. Nós podemos usa-los para fazer qualquer coisa desde valores booleanos e enumeradores para dias de semana para árvores de busca binária e muito mais!

Typeclasses 102

Até agora, temos aprendido sobre algumas das typeclasses padrões de Haskell e temos visto quais tipos estão nelas. Também temos aprendido como criar automáticamente nossas próprias instâncias de tipo a partir das typeclasses padrões por pedir a Haskell para que derive as instâncias para nós. Nessa seção, vamos aprender como criar nossas próprias typeclasses e como criar instâncias de tipo delas na mão.

Uma recapitulação rápida sobre typeclasses: typeclasses são como interfaces. Uma typeclass define algum comportamento (como comparação para igualdade, comparação para ordenação, enumeração) e daí tipos que podem agir de tal forma são feitas instâncias daquela typeclass. O comportamento de typeclasses é alcançado definindo-se funções ou apenas declarações de tipo que então nós implementamos. Então quando dizemos que um tipo é uma instância de uma typeclass, queremos dizer que podemos usar as funções que tal typeclass define com aquele tipo.

Typeclasses não têm nada a ver com classes de linguagens como Java ou Python. Isso confunde muita gente, então eu quero que você esqueça tudo que sabe até agora de classes em linguagens imperativas exatamente agora.

Por exemplo, a typeclass Eq é para coisas que podem ser igualadas. Ela define as funções == e /=. Se nós tivermos um tipo (digamos, Car) e a comparação entre dois carros com a função de igualdade == fizer sentido, então faz sentido que Car seja uma instância de Eq.

É assim que a classe Eq está definida no prelúdio padrão:

class Eq a where
    (==) :: a -> a -> Bool
    (/=) :: a -> a -> Bool
    x == y = not (x /= y)
    x /= y = not (x == y)

Opa, opa, opa! Sintaxe e palavras-chave estranhas apareceram aí! Não se preocupe, isso ficará totalmente claro em alguns segundos. Primeiramente, quando escrevemos class Eq a where, isso significa que estamos definindo uma typeclass nova e que é chamada Eq. O a é a variável de tipo e ela significa que a terá o papel do tipo que logo será uma insância de Eq. Isso não tem que ser chamado a, não tem nem que ser apenas uma letra, tem apenas que ser uma palavra apenas com letras minúsculas. Daí, definimos várias funções. Não é mandatório implementar os corpos das funções, temos apenas de especificar as declarações de tipo para as funções.

De qualquer forma, nós de fato implementamos o corpo das funções que Eq define, mas nós o definimos em termos de recursão mútua. Dissemos que duas instâncias de Eq são iguais se elas não forem diferentes e são diferentes se não forem iguais. Não tínhamos de fazer isso, sério, mas fizemos e vamos ver como isso nos ajudará posteriormente.

Então, uma vez que temos uma classe, o que podemos fazer com ela? Bem, não muito, na realidade. Mas quando começamos a fazer instâncias de tipo dessa classe, começamos a ganhar algumas funcionalidades legais. Com isso, observe esse tipo:

data TrafficLight = Red | Yellow | Green

Ele define os estados de um semáforo. Perceba como não derivamos nenhuma instância de classe para tal. Então uma vez que vamos escrever algumas instanciações na mão, mesmo podendo derivá-las de tipos como Eq e Show. Aqui está como fazemos uma instância de Eq.

instance Eq TrafficLight where
    Red == Red = True
    Green == Green = True
    Yellow == Yellow = True
    _ == _ = False

Nós fizemos isso usando a palavra-chave instance. Então class é para se definir novas typeclasses e instance é para se fazer novas instâncias de tipos a partir de typeclasses. Quando estávamos definindo Eq, escrevemos class Eq a where e dissemos que a tem o papel de representar o tipo do qual será feita uma instância mais tarde. Podemos ver isso claramente aqui porque quando estamos criando uma instância, escrevemos instance Eq TrafficLight where. Substituímos o a com o tipo de verdade.

Uma vez que == foi definido em termos de /= e vice-versa na declaração class, tivemos apenas de sobrescrever um deles na declaração da instância. Isso se chama definição completa mínima da typeclass — o mínimo de funções que temos de implementar para que nosso tipo possa se comportar como a classe informa. Para cumprir a definição mínima completa para Eq, temos de sobrescrever ou == ou /=. Se Eq fosse definido simplesmente assim:

class Eq a where
    (==) :: a -> a -> Bool
    (/=) :: a -> a -> Bool

teríamos de implementar ambas as funções quando estivéssemos criando as instâncias dos tipos, uma vez que Haskell não saberia como estas duas funções estariam relacionadas. A definição mínima completa seria então: ambos == e /=.

Você pode ver que implementamos == simplesmente fazendo casamento de padrões. Já que existem mais casos onde duas luzes não são iguais, especificamos os que são iguais e então fizemos um padrão mais geral dizendo que se não for nenhuma das combinações anteriores, então duas luzes não são iguais.

Vamos criar uma instância de Show na mão, também. Para satisfazer a definição completa mínima para Show, temos apenas de implementar sua função show, que recebe um valor e o transforma em uma string.

instance Show TrafficLight where
    show Red = "Red light"
    show Yellow = "Yellow light"
    show Green = "Green light"

Mais uma vez, usamos casamento de padrões para alcançar nossos objetivos. Vamos ver como isso funciona na prática:

ghci> Red == Red
True
ghci> Red == Yellow
False
ghci> Red `elem` [Red, Yellow, Green]
True
ghci> [Red, Yellow, Green]
[Red light,Yellow light,Green light]

Legal. Poderíamos ter simplesmente derivado Eq e teríamos tido o mesmo efeito (mas não o fizemos por propósitos educacionais). Entretanto, derivar Show teria sido apenas traduzir diretamente o valor dos construtores para strings. Mas se quisermos que as luzes apareçam como "Red light", então temos que fazer a declaração da instância na mão.

Você pode também fazer typeclasses que são subclasses de outras typeclasses. A declaração class para Num é um pouco longa, mas aqui vai a primeira parte:

class (Eq a) => Num a where
   ...  

Como mencionamos anteriormente, há muitos lugares onde podemos amontoar restrições de classe. Isso é como escrever class Num a where, mas assim dizemos que nosso tipo a deve ser uma instância de Eq. Estamos essencialmente dizendo que temos de fazer uma instância de tipo de Eq antes que possamos torná-la uma instância de Num. Antes que algum tipo possa ser considerado um número, faz sentido que possamos determinar se valores de tal tipo podem ser igualados ou não. Isso é realmente tudo que temos em subclasses, é apenas uma restrição de classe numa declaração class! Ao definir o corpo de funções na declaração class ou quando definindo-as nas declarações instance, podemos assumir que a é parte de Eq e então podemos usar == em valores desse tipo.

Mas como são os tipos Maybe ou listas feitas instâncias de typeclasses? O que faz Maybe diferente de, digamos, TrafficLight, é que Maybe por si só não é um tipo concreto, é um construtor de tipo que recebe um parâmetro de tipo (como Char ou algo do tipo) para produzir um tipo concreto (like Maybe Char). Vamos dar uma olhada na typeclass Eq novamente:

class Eq a where
    (==) :: a -> a -> Bool
    (/=) :: a -> a -> Bool
    x == y = not (x /= y)
    x /= y = not (x == y) 

Pela declaração dos tipos, vemos que a é usado como tipo concreto porque todos os tipos em funções têm que ser concretos (lembre-se, você não pode ter uma função do tipo a -> Maybe mas você pode ter uma função do tipo a -> Maybe a ou Maybe Int -> Maybe String). Por isso não podemos fazer algo do tipo

instance Eq Maybe where
    ...  

Porque como nós vimos, o a tem de ser um tipo concreto, masMaybe não é concreto. É um construtor de tipo que recebe um parâmetro e então produz um tipo concreto. Também seria entediante escrever instance Eq (Maybe Int) where, instance Eq (Maybe Char) where, etc. para todo, todo tipo. Então poderíamos escrevê-lo como:

instance Eq (Maybe m) where
    Just x == Just y = x == y
    Nothing == Nothing = True
    _ == _ = False
      

Isso é como se disséssemos que queremos que todos os tipos da forma Maybe something sejam uma instância de Eq. Na verdade poderíamos ter escrito (Maybe something), mas geralmente optamos por letras singulares para nos manter fiéis ao estilo de Haskell. O (Maybe m) aqui tem o papel do a de class Eq a where. Enquanto que Maybe não é um tipo concreto, Maybe m é. Por especificar um parâmetro de tipo (m, que está com todas as letras em minúsculo), dissemos que queremos todos os tipos que estão na forma Maybe m, onde m é qualquer tipo, para ser uma instância de Eq.

Há, entretanto, um problema com isso. Consegue encontrá-lo? Nós usamos == no conteúdo de Maybe mas não temos garantias de que o que Maybe contém pode ser usado comEq! Por isso temos que modificar nossa declaração instance assim:

instance (Eq m) => Eq (Maybe m) where
    Just x == Just y = x == y
    Nothing == Nothing = True
    _ == _ = False
      

Tivemos de declarar uma restrição de classe! Com essa declaração instance, dizemos isso: queremos que todos os tipos na forma Maybe m sejam parte da typeclass Eq, mas apenas se esses tipos fossem o m (dessa forma o que estivesse contido dentro de Maybe) também seria parte de Eq. Na verdade isso é também como Haskell deriva a instância.

Na maioria das vezes, restrições de classe em declarações class são utilizadas para tornar uma typeclass uma subclasse de outra typeclass e as restriçõees de classe em declarações instance são utilizadas para expressar requisitos sobre os conteúdos de algum tipo. Por exemplo, aqui nós precisávamos que o conteúdo do Maybe também fosse parte da typeclass Eq.

Ao se criar instâncias, se você notar que um tipo é usado como um tipo concreto nas declarações de tipo (como o a em a -> a -> Bool), você deve suprir parâmetros de tipo e adicionar parênteses para se obter um tipo concreto.

Eeita, mais uma coisa, olha! Se você quiser ver quais são as instâncias de uma typeclass, apenas digite :info YourTypeClass no GHCI. Então digitar :info Num mostrará que funções a typeclass define e te dará uma lista dos tipos da typeclass. :info funciona também para tipos e construtores de tipos. Se você fizer :info Maybe, ele te mostrara todas as typeclasses das quais Maybe é uma instância. E também, :info pode te mostrar a declaração de tipo de uma função. Eu acho que isso é muito massa.

Uma typeclass sim-não

Em JavaScript e outras linguagens fracamente tipadas, você pode pôr quase qualquer coisa dentro de uma expressão. Por exemplo, você pode fazer tudo o que se segue: if (0) alert("YEAH!") else alert("NO!"), if ("") alert ("YEAH!") else alert("NO!"), if (false) alert("YEAH") else alert("NO!), etc. e todos esses vão mandar um alerta de NO!. Se você fizer if ("WHAT") alert ("YEAH") else alert("NO!"), vai alertar um "YEAH!" porque JavaScript considera palavras não vazias como tendo um valor meio verdadeiro.

Mesmo que o uso estrito de Bool para semânticas booleanas funcione melhor em Haskell, vamos tentar implementar aquele comportamento meio JavaScript. Por diversão! Vamos começar com uma declaração class.

class YesNo a where
    yesno :: a -> Bool

Muito simples. A typeclass YesNo define uma função. Tal função pega um valor de um tipo que é considerado conter algum valor de verdade e nos diz com certeza se é verdadeiro ou não. Note que da forma como utilizamos a na função, a tem que ser um tipo concreto.

Agora, vamos definir algumas instâncias. Para números, vamos assumir que (como em JavaScript) qualquer número que não seja 0 é verdadeiro e 0 é falso.

instance YesNo Int where
    yesno 0 = False
    yesno _ = True

Listas vazias (e por extensão, strings) são valores negativos, enquanto que listas não-vazias são valores verdadeiros.

instance YesNo [a] where
    yesno [] = False
    yesno _ = True

Note como acabamos de pôr um parâmetro de tipo a lá para tornar a lista um tipo concreto, mesmo que não façamos nenhuma suposição sobre o tipo que está contido na lista. O que mais, hmm... já sei, o próprio Bool guarda verdade e falsidade, e é bem óbvio qual é qual.

instance YesNo Bool where
    yesno = id   

Han? O que é id? É apenas uma função padrão da biblioteca que pega um parâmetro e retorna a mesma coisa, que é o que estaríamos escrevendo de qualquer forma.

Vamos tornar Maybe a uma instância também.

instance YesNo (Maybe a) where
    yesno (Just _) = True
    yesno Nothing = False

Nós não precisamos de uma restrição de classe porque não fizemos nenhuma suposição sobre o conteúdo de Maybe. Apenas dissemos que é verdadeiro se for um valor Just e falso se for um Nothing. Ainda tivemos de escrever (Maybe a) ao invés de apenas Maybe porque, se você parar pra pensar, uma função Maybe -> Bool não pode existir (porque Maybe não é um tipo concreto), onde que Maybe a -> Bool está bem e elegante. Ainda sim, isso é muito legal porque, agora, qualquer tipo na forma Maybe something é parte de YesNo e não importa o que something é.

Anteriormente, definimos um tipoTree a, que representava uma árvore de busca binária. Podemos dizer que uma árvore vazia é falsa e qualquer coisa que não seja vazia seja verdadeira.

instance YesNo (Tree a) where
    yesno EmptyTree = False
    yesno _ = True

Um semáforo pode ter um valor de sim ou não? Certamente. Se for vermelho, você para. Se for verde, você vai. Se for amarelo? Eh, eu geralmente ultrapasso amarelos porque eu vivo para a adrenalina.

instance YesNo TrafficLight where
    yesno Red = False
    yesno _ = True

Legal, agora que temos algumas instâncias, vamos brincar!

ghci> yesno $ length []
False
ghci> yesno "haha"
True
ghci> yesno ""
False
ghci> yesno $ Just 0
True
ghci> yesno True
True
ghci> yesno EmptyTree
False
ghci> yesno []
False
ghci> yesno [0,0,0]
True
ghci> :t yesno
yesno :: (YesNo a) => a -> Bool

Certo, funciona! Vamos fazer uma função que imita o if, mas funciona com valores YesNo.

yesnoIf :: (YesNo y) => y -> a -> a -> a
yesnoIf yesnoVal yesResult noResult = if yesno yesnoVal then yesResult else noResult

Bem direto ao ponto. Precisa de um valor sim-ou-não e duas coisas. Se o valor s-m-ou-não for mais pra um sim, retorna a primeira das duas coisas, caso contário, retorna a segunda delas.

ghci> yesnoIf [] "YEAH!" "NO!"
"NO!"
ghci> yesnoIf [2,3,4] "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf True "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf (Just 500) "YEAH!" "NO!"
"YEAH!"
ghci> yesnoIf Nothing "YEAH!" "NO!"
"NO!"

A typeclass Functor

Até agora, nós temos encontrado diversas typeclasses na biblioteca padrão. Nós brincamos com Ord, que é feito para coisas que podem ser ordenadas. Nós fizemos amizade com Eq, que é feito para coisas que podem ser igualadas. Nós vimos Show, que serve de interface para tipos nos quais seus valores podem ser mostrados como strings. Nosso bom amigo Read está aqui sempre que nós precisamos converter uma string para um valor de algum tipo. E agora, nós vamos dar uma olhada no código da typeclass Functor, que é basicamente para coisas que podem ser mapeadas. Você provavelmente está pensando em listas, já que mapeamento sobre listas é um idioma dominante em Haskell. E você está certo, o tipo list é parte do typeclass Functor.

Que maneira melhor de conhecer o typeclass Functor do que ver como ele é implementado? Vamos dar uma olhada.

class Functor f where
    fmap :: (a -> b) -> f a -> f b

OK. Nós vimos que ele define uma função, fmap, e não fornece nenhuma implementação padrão para ela. O tipo de fmap é interessante. Na definição de typeclasses até agora, a variável 'type' que agiu como o type em typeclass foi um tipo concreto, como o a em (==) :: (Eq a) => a -> a -> Bool. Mas agora, o f não é um tipo concreto (um tipo que um valor pode ter, como Int, Bool ou Maybe String), mas sim um construtor de tipos que pegue um parâmetro de tipo. Um exemplo pra refrescar a memória: Maybe Int é um tipo concreto, mas Maybe é um construtor de tipo que pega um tipo como parâmetro. De qualquer modo, nós vimos que fmap pega uma função de um tipo para outro e um functor aplicado em um tipo e retorna um functor aplicado ao outro tipo.

Se isso soa um pouco confuso, não se preocupe. Tudo será revelado em breve quando nós observamos alguns exemplos. Humm, essa declaração de tipo de fmap me lembra de alguma coisa. Se você não sabe qual é a assinatura de tipo de map , é essa: map :: (a -> b) -> [a] -> [b].

Ah, interessante! Ele pega uma função de um tipo para outro e uma lista de um tipo e retorna uma lista do outro tipo. Meus amigos, eu acho que nós temos um functor! De fato, map é só um fmap que só funciona com listas. Aqui está a prova de que list é uma instância do typeclass Functor.

instance Functor [] where
    fmap = map

É isso! Perceba como nós não escrevemos instance Functor [a] where, porque de fmap :: (a -> b) -> f a -> f b, nós vemos que f tem que ser um construtor de tipo que pegue um tipo. [a] já é um tipo concreto (de uma lista com qualquer tipo dentro dela), enquanto que [] é um construtor de tipo que pega um tipo e pode produzir tipos como [Int], [String] ou mesmo [[String]].

Já que para listas, fmap é só map, nós temos os mesmos resultados quando usamos eles em listas.

map :: (a -> b) -> [a] -> [b]
ghci> fmap (*2) [1..3]
[2,4,6]
ghci> map (*2) [1..3]
[2,4,6]

O que acontece quando nós usamos map ou fmap em uma lista vazia? Bom, com certeza nós obtemos uma lista vazia. Isso só torna uma lista vazia do tipo [a] em uma lista vazia do tipo [b].

Tipos que podem agir como uma caixa podem ser functors. Você pode pensar numa lista como uma caixa que tem uma quantidade infinita de pequenos compartimentos e eles podem estar todos vazios, um pode estar cheio e os outros vazios ou um conjunto deles pode estar cheio. Então, o que mais tem a propriedade de ser como uma caixa? Por exemplo, o tipo Maybe a. De certo modo, é como uma caixa que pode não ter nada, nesse caso ela tem o valor Nothing, ou ela pode ter um item, como "HAHA", e nesse caso ela tem o valor Just "HAHA". Aqui está como Maybe é um functor.

instance Functor Maybe where
    fmap f (Just x) = Just (f x)
    fmap f Nothing = Nothing

Novamente, perceba como nós escrevemos instance Functor Maybe where ao invés de instance Functor (Maybe m) where, como nós fizemos quando estávamos lidando com Maybe e YesNo. Functor quer um construtor de tipo que pegue um tipo e não um tipo concreto. Se você mentalmente trocar os f pelos Maybe, fmap age como um (a -> b) -> Maybe a -> Maybe b para esse tipo particular, o que parece OK. Mas se você trocar f por (Maybe m), então ele parece agir como (a -> b) -> Maybe m a -> Maybe m b, o que não faz nenhum sentido porque Maybe só pega um parâmetro de tipo.

De qualquer modo, a implementação de fmap é bem simples. Se ele é um valor vazio de Nothing, então só retorne um Nothing. Se nós mapearmos sobre uma caixa vazia, nós temos uma caixa vazia. Isso faz sentido. Do mesmo jeito, se nós mapearmos sobre uma lista vazia, nós temos uma lista vazia. Se isso não é um valor vazio, mas sim um simples valor encapsulado em um Just, então nós aplicamos a função no conteúdo de Just.

ghci> fmap (++ " HEY GUYS IM INSIDE THE JUST") (Just "Something serious.")
Just "Something serious. HEY GUYS IM INSIDE THE JUST"
ghci> fmap (++ " HEY GUYS IM INSIDE THE JUST") Nothing
Nothing
ghci> fmap (*2) (Just 200)
Just 400
ghci> fmap (*2) Nothing
Nothing

Outra coisa que pode ser mapeada e criar uma instância de Functor é o nosso tipo Tree a. Isso pode ser pensado como uma caixa em um caminho (com algum ou nenhum valor) e o construtor de tipo Tree pega exatamente um parâmetro de tipo. Se você olhar para fmap como se isso fosse uma função feita apenas para Tree, sua assinatura de tipo pode parecer com (a -> b) -> Tree a -> Tree b. Nós vamos usar recursão nesse tipo. Mapear uma árvore vazia produz uma árvore vazia. Mapear uma árvore não-vazia vai produzir uma árvore consistindo da nossa função aplicada ao valor da raiz e suas sub-árvores da direita e da esquerda serão as sub-árvores anteriores, só a nossa função será mapeada sobre elas.

instance Functor Tree where
    fmap f EmptyTree = EmptyTree
    fmap f (Node x leftsub rightsub) = Node (f x) (fmap f leftsub) (fmap f rightsub)

ghci> fmap (*2) EmptyTree
EmptyTree
ghci> fmap (*4) (foldr treeInsert EmptyTree [5,7,3,2,1,7])
Node 28 (Node 4 EmptyTree (Node 8 EmptyTree (Node 12 EmptyTree (Node 20 EmptyTree EmptyTree)))) EmptyTree

Legal! Agora que tal Either a b? Isso pode ser um functor? O typeclass Functor quer um construtor de tipo que pegue somente um parâmetro de tipo mas Either pega dois. Hummm! Eu sei, nós estamos aplicando parcialmente Either alimentando ele só com um parâmetro o que o deixa com um parâmetro livre. Aqui está como Either a é um functor nas bibliotecas padrão:

instance Functor (Either a) where
    fmap f (Right x) = Right (f x)
    fmap f (Left x) = Left x

Bem bem, o que nós fizemos aqui? você pode ver como nós fizemos Either a uma instância ao invés de só Either. Isso acontece porque Either a é um construtor de tipo que pega um parâmetro, enquanto que Either pega dois. Se fmap fosse especificamente para Either a, a assinatura de tipos seria então (b -> c) -> Either a b -> Either a c porque isso é o mesmo que (b -> c) -> (Either a) b -> (Either a) c. Na implementação, nós mapeamos o caso de um construtor de valor Right, mas nós não fizemos isso no caso do Left. Por que isso? Bom, se nós olharmos de volta como o tipo Either a b é definido, é meio que:

data Either a b = Left a | Right b

Bom, se nós quisermos mapear uma função sobre ambas, a e b devem ser do mesmo tipo. Ou seja, Se nós tentarmos mapear uma função que pega uma string e retorna uma string e o b como uma string mas o a como um número, isso não iria realmente funcionar. Além disso, vendo o que o tipo de fmap seria se isso operasse só com valores Either, nós vemos que o primeiro parâmetro tem que permanecer o mesmo enquanto o segundo pode mudar e o primeiro parâmetro é atualizado pelo construtor de valor Left.

Isso também funciona bem com nossa analogia de caixa se nós pensarmos na parte Left como uma espécie de uma caixa vazia com uma mensagem de erro escrita do lado nos dizendo porque ela está vazia.

Mapas de Data.Map também podem fazer um functor porque eles guardam valores (ou não!). No caso de Map k v, fmap vai mapear uma função v -> v' sobre um mapa do tipo Map k v e retornar um mapa do tipo Map k v'.

Tente imaginar como Map k é uma instância de Functor por si mesmo!

Com a typeclass Functor, nós vimos como typeclasses podem representar conceitos de alta ordem bem legais. Nós também tivemos alguma prática com tipos parcialmente aplicáveis e criação de instâncias. Em um dos próximos capítulos, nós também vamos dar uma olhada em algumas regras que se aplicam para functors.

Tipos e algumas classes-foo

Construtores de tipos pegam outros tipos como parâmetros para eventualmente produzir tipos concretos. Isso meio que me lembra de funções, que pega valores como parâmetros para produzir valores. Nós vimos que esses construtores de tipo podem ser parcialmente aplicados (Either String é um tipo que pega um tipo e produz um tipo concreto, como Either String Int), assim como as funções podem. Isso é, de fato, muito interessante. Nessa seção, nós daremos uma olhada na definição formal de como tipos são aplicados a construtores de tipos, assim como nós demos uma olhada em como definir formalmente como valores são aplicados a funções usando declarações de tipo. Você não precisa realmente ler essa seção para continuar sua jornada mágica em Haskell e se você não entender isso, não se preocupe. Porém, entender isso vai te dar um conhecimento muito profundo do sistema de tipos.

Então, valores como 3, "YEAH" ou takeWhile (funções também são valores, porque nós podemos passar elas como parâmetro) têm cada um seu próprio tipo. Tipos são pequenos rótulos que os valores carregam para que nós possamos pensar a respeito dos valores. Mas os tipos têm seus próprios rótulos, chamados classes. Uma classe é mais ou menos um tipo de tipo. Isso pode soar um pouco estranho e confuso, mas é de fato um conceito muito legal.

O que são classes e pra que elas servem? Bem, vamos examinar a classe de um tipo usando o comando :k no GHCI.

ghci> :k Int
Int :: *

Uma estrela? Que exótico. O que isso significa? Uma * significa que o tipo é um tipo concreto. Um tipo concreto é um tipo que não pega nenhum parâmetro de tipo e os valores só podem ter tipos que são tipos concretos. Se eu tiver que ler * em voz alta (eu nunca tive que fazer isso até hoje), eu diria estrela ou só tipo.

Ok, agora vamos ver qual a classe de Maybe.

ghci> :k Maybe
Maybe :: * -> *

O construtor de tipo Maybe pega um tipo concreto (como Int) e depois retorna um tipo concreto como Maybe Int. E é isso que essa classe nos diz. Assim como Int -> Int significa que uma função pega um Int e retorna um Int, * -> * significa que o construtor de tipos pega um tipo concreto e retorna um tipo concreto. Vamos aplicar o parâmetro de tipo ao Maybe e ver qual a classe desse tipo.

ghci> :k Maybe Int
Maybe Int :: *

Exatamente como eu esperava! Nós aplicamos o parâmetro de tipo ao Maybe e recebemos de volta um tipo concreto (é isso o que * -> * significa. Um paralelo (embora não seja equivalente, tipos e classes são duas coisas diferentes) a isso é se nós fizermos :t isUpper and :t isUpper 'A'. isUpper tem como tipo Char -> Bool e isUpper 'A' tem como tipo Bool, porque seu valor é basicamente False. Ambos os tipo, porém, têm uma espécie de *.

Nós usamos :k em um tipo para obter sua classe, assim como nós podemos usar :t em um valor para obter seu tipo. Como nós dissemos, tipos são os rótulos dos valores e classes são os rótulos dos tipos e existem paralelos entre os dois.

Vamos olhar para outra classe.

ghci> :k Either
Either :: * -> * -> *

Arrá, isso nos diz que Either pega dois tipos concretos como parâmetros de tipo para produzir um tipo concreto. Isso também se parece com uma declaração de tipo de uma função que pega dois valores e retorna alguma coisa. Construtores de tipo são curriadas (assim como funções), assim nós podemos aplicá-las parcialmente.

Either String :: * -> *
ghci> :k Either String Int
Either String Int :: *

Quando nós queríamos fazer de Either uma parte da typeclass de Functor, nós tínhamos que aplicá-la parcialmente porque Functor requer tipos que pegam somente um parâmetro enquanto que Either pega dois. Em outras palavras, Functor requer tipos da classe * -> * e então nós teremos que aplicar parcialmente Either para obter um tipo da classe * -> * ao invés da sua classe original, * -> * -> *. Se nós olharmos para a definição de Functor de novo

class Functor f where 
    fmap :: (a -> b) -> f a -> f b

nós vemos que a variável de tipo f é usada como um tipo que pega um tipo concreto para produzir um tipo concreto. Nós sabemos que isso tem que produzir um tipo concreto porque isso é usado como o tipo de um valor em uma função. E disso, nós podemos deduzir que tipos que quiserem ser amigos de Functor têm que ser da classe * -> *.

Agora, vamos ver algumas classes-foo. Dê uma olhada nessa typeclass que eu vou fazer agora:

class Tofu t where
    tofu :: j a -> t a j

Cara, isso parece estranho. Como vamos fazer um tipo que pode ser uma instância dessa estranha typeclass? Bom, vamos olhar no que a sua classe deveria ser. Pelo fato de j a ser usado como o tipo de um valor que a função tofu pega como seu parâmetro, j a tem ser da classe *. Nós assumimos * para a e então nós podemos inferir que j tem que ser da classe * -> *. Nós vemos que t tem que produzir um valor concreto também e que ele pega dois tipos. E sabendo que a é da classe * e j é da classe * -> *, nós inferimos que t tem que ser da classe * -> (* -> *) -> *. Então ele pega um tipo concreto (a), um construtor de tipos que pega um tipo concreto (j) e produz um tipo concreto. Uau.

OK, vamos fazer um tipo com a classe * -> (* -> *) -> *. Aqui está uma maneira de fazer isso.

data Frank a b  = Frank {frankField :: b a} deriving (Show)

Como nós sabemos que esse tipo é da classe * -> (* -> *) - > *? Bem, campos em ADTs são feitos para guardar valores, então eles devem ser da classe *, obviamente. Nós assumimos * para a, o que significa que b pega um parâmetro de tipo e então sua classe é * -> *. Agora nós sabemos as classes de ambos a e b e como eles são parâmetros para Frank, nós vimos que Frank é da classe * -> (* -> *) -> *. O primeiro * representa a e o (* -> *) representa b. Vamos fazer algums valores Frank e verificar seus tipos.

ghci> :t Frank {frankField = Just "HAHA"}
Frank {frankField = Just "HAHA"} :: Frank [Char] Maybe
ghci> :t Frank {frankField = Node 'a' EmptyTree EmptyTree}
Frank {frankField = Node 'a' EmptyTree EmptyTree} :: Frank Char Tree
ghci> :t Frank {frankField = "YES"}
Frank {frankField = "YES"} :: Frank Char []

Humm. Como frankField tem um tipo da forma a b, seus valores tem que ter tipos que tem uma forma similar. Então eles podem ser Just "HAHA", que é do tipo Maybe [Char] ou ele pode ter o valor ['Y','E','S'], que é do tipo [Char] (se nós usássemos nossa própria lista para isso, ele seria do tipo List Char). E nós vemos que os tipos dos valores de Frank correspondem com a classe de Frank. [Char] é da classe * e Maybe é da classe * -> *. Para se obter um valor, isso tem que ser um tipo concreto e ainda tem que ser completamente aplicado, pois todo valor de Frank blah blaah é da classe *.

Tornar Frank uma instância de Tofu é bem simples. Nós vemos que tofu pega um j a (logo um exemplo de tipo dessa forma seria Maybe Int) e retorna um t a j. Logo, se nós trocarmos Frank por j, o tipo do resultado seria Frank Int Maybe.

instance Tofu Frank where
    tofu x = Frank x

ghci> tofu (Just 'a') :: Frank Char Maybe
Frank {frankField = Just 'a'}
ghci> tofu ["HELLO"] :: Frank [Char] []
Frank {frankField = ["HELLO"]}

Não muito útil, mas nós flexionamos nossos 'músculos de tipo'. Vamos fazer alguns outros tipo-foo. Nós temos esse tipo de dado:

data Barry t k p = Barry { yabba :: p, dabba :: t k }

E agora nós queremos fazer dele uma instância de Functor. Functor requer tipos da classe * -> * mas Barry não parece ser dessa classe. Qual a classe de Barry? Bem, nós vemos que ele pega três parâmetros de tipo, então ele será something -> something -> something -> *. É seguro dizer que p é um tipo concreto e que é da classe *. Para k, nós assumimos * e por extensão, t é da classe * -> *. Agora vamos apenas trocar essas classes pelo somethings que usamos como placeholders e veremos se é da classe (* -> *) -> * -> * -> *. Vamos checar com o GHCI.

ghci> :k Barry
Barry :: (* -> *) -> * -> * -> *

Ah, estávamos certos. Que satisfatório. Agora, para fazer disso uma parte de Functor, nós temos que aplicar parcialmente os dois primeiros parâmetros de tipo e assim só nos resta * -> *. Isso significa que o começo de uma declaração de instância será: instance Functor (Barry a b) where. Se nós olharmos para fmap como se ele fosse feito especificamente para Barry, ele seria do tipo fmap :: (a -> b) -> Barry c d a -> Barry c d b, porque nós só trocamos o f do Functor pelo Barry c d. O terceiro tipo de parâmetro de Barry terá que mudar e nós vemos que isso está convenientemente no seu campo.

instance Functor (Barry a b) where
    fmap f (Barry {yabba = x, dabba = y}) = Barry {yabba = f x, dabba = y}

Aqui vamos nós! Nós acabamos de mapear o f sobre o primeiro campo.

Nessa seção, nós demos uma boa olhada em como parâmetros de tipo funcionam e meio que formalizamos eles com classes, assim como nós formalizamos parâmetros de função com declaração de tipos. Nós vimos que existem paralelos interessantes entre funções e construtores de tipos. Eles são, porém, duas coisas completamente diferentes. Quando trabalhar com Haskell de verdade, você normalmente não vai se confundir com classes e fará inferência de classes na mão como nós fizemos agora. Normalmente, você só tem que aplicar parcialmente seu próprio tipo em * -> * ou * quando for fazer uma instância de uma das typeclasses padrão, mas é bom saber como e porquê isso de fato funciona. Também é interessante ver que tipos tem seus próprios pequenos tipos. De novo, você não precisa entender tudo que fizemos aqui para continuar a leitura, mas se você entendeu como classes funcionam, você provavelmente tem uma base muito sólida do sistema de tipos de Haskell.