Resolvendo Problemas Funcionalmente

Neste capítulo, iremos dar uma olhada em alguns problemas interessantes e como pensar funcionalmente para resolvê-los tão elegantemente quanto possível. Nós provavelmente não introduziremos nenhum novo conceito, apenas iremos ser flexíveis com nossos recém-adquiridos músculos de Haskell e praticar nossas habilidades de codar. Cada sessão irá apresentar um problema diferente. Primeiro vamos descrever o problema, em seguida iremos tentar encontrar a melhor (ou menos pior) forma de resolve-lo.

Calculadora de Notação Polonesa Inversa

Normalmente quando nós escrevemos expressões matemáticas na escola, nós as escrevemos de uma maneira infixada. Por exemplo, nós escrevemos 10 - (4 + 3) * 2. +, * e - são operadores infixos, da mesma forma que funções infixadas que nos encontramos em Haskell (+, `elem`, etc.). Isto torna tudo mais prático para nós, como humanos podemos facilmente realizar o parser em nossas mentes apenas olhando qual é a expressão. A desvantagem disto é que nós temos de usar parênteses para denotar a precedência.

Notação Polonesa Inversa é uma outra forma de escrever matematicamente expressões. Inicialmente isso pode soar estranho, mas esta é atualmente a forma mais fácil de entender e usar porque não é necessário usar parênteses e é muito fácil de colocar isso em uma calculadora. Enquanto muitas das calculadoras modernas usam notação infixa, algumas pessoas continuam usando calculadoras NPI. É assim que a expressão infixa previamente mostrada parece na NPI: 10 4 3 + 2 * -. Como podemos calcular qual o resultado disso? Bem, pense em uma pilha. Quando nós encontramos um operador, pegamos os dois números que estão no topo da pilha (também dizemos que estamos fazendo um pop), usamos o operador, os dois números, por fim colocamos o número resultante de volta à pilha. Quando você encontrar o fim de uma expressão, você estará com um único número se a expressão foi bem formada e este número representa o resultado.

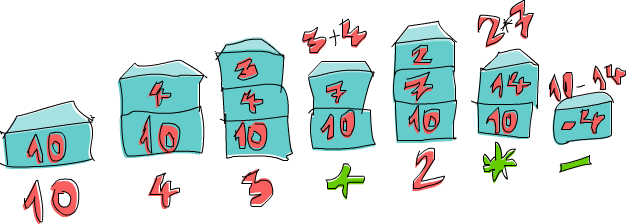
Vamos analisar a expressão 10 4 3 + 2 * - juntos! Primeiro nós colocamos 10 na pilha e a pilha agora está assim 10. O próximo item é 4 então colocamos ele na pilha também. A pilha agora esta assim 10, 4. Fazemos a mesma coisa com 3 e agora a pilha ficou assim 10, 4, 3. Finalmente encontramos uma operação, o nosso conhecido +! Então pegamos os dois números do topo da pilha (ficando a pilha apenas com o 10), adicionamos estes números e devolvemos o resultado da operação à pilha. A pilha agora esta assim 10, 7. Nós colocamos 2 na pilha, e a pilha agora está assim 10, 7, 2. Nós então encontramos um operador novamente, então vamos pegar o 7 e 2 da pilha, multiplicamos e então colocamos o resultado na pilha. Multiplicando 7 e 2 produz um 14, então a pilha que nós temos agora está assim 10, 14. Finalmente, há um -. Nós pegamos o 10 e o 14 da pilha, subtraímos 14 de 10 e então colocamos o resultado de volta. O número na pilha agora é -4 e como não há mais nenhum número ou operador em nossa expressão, este é nosso resultado!

Agora que nós sabemos como nós podemos calcular qualquer expressão NPI manualmente, vamos pensar como nós podemos fazer uma função de Haskell que pega essa expressão como uma string que contém uma expressão NPI, como "10 4 3 + 2 * -" e nos devolve o resultado.

Qual pode ser o tipo desta função? Nós queremos pegar uma string como parâmetro e produzir um número como resultado. Então provavelmente será algo como solveRPN :: (Num a) => String -> a.

Dica útil: realmente ajuda primeiro pensar qual o tipo que a função declarada pode ser antes de nós mesmos escrevermos a implementação. Em Haskell, a declaração do tipo de uma função nos diz muito sobre a função, devido ao sistema de tipos muito forte de Haskell.

Legal. Ao implementar uma solução para um problema em Haskell, é bom pensar um pouco e como você pode fazer isso manualmente e talvez tentar ver se você pode ter alguma inspiração de como fazer. Aqui vemos que nós tratamos cada número ou operador que estava separado por um espaço como um item único. Então isto pode nos ajudar se nós queremos começar a quebrar uma string como "10 4 3 + 2 * -" em uma lista de itens como ["10","4","3","+","2","*","-"].

Logo a seguir, o que vamos fazer com essa lista de itens em nossas cabeças? Nós queremos ir sobre ela da esquerda pra direita e manter uma pilha do que estávamos fazendo. A sentença anterior lembra você de alguma coisa? Lembre-se, na sessão sobre folds, nós dissemos que uma forma bonita para qualquer função que atravessa os elementos de uma lista da esquerda pra direita ou da direita pra esquerda elemento por elemento e constrói (acumula) algum resultado (se este é um número, uma lista, uma pilha, seja lá o que for) pode ser implementado com um fold.

Neste caso, nós iremos usar um left fold, porque nós iremos sobre a lista da esquerda pra direita. O valor do acumulador irá ser nossa pilha e, portanto, o resultado do nosso fold também será uma pilha, e assim como nós vimos, ela terá apenas um item.

Mais uma coisa para pensar sobre: como iremos representar uma pilha? Eu proponho que nós usemos uma lista. Também proponho de preservarmos o topo da pilha na cabeça dela. Isto porque adicionando na cabeça (começo) da lista é muito mais rápido do que adicionar ao fim dela. Então se nós temos uma pilha, digamos, 10, 4, 3, nós iremos representa-lá como uma lista [3,4,10].

Agora nós temos informação suficiente para esboçar aproximadamente como será a nossa função. Vamos pegar uma string, como "10 4 3 + 2 * -" e quebrá-la em uma lista de itens usando words para obter ["10","4","3","+","2","*","-"]. A seguir, nós iremos fazer um left fold sobre esta lista e terminar com uma pilha que tem apenas um elemento, que é [-4]. Nós pegamos este único item da lista e então este é o nosso resultado final.

Então aqui está o esqueleto da função:

import Data.List

solveRPN :: (Num a) => String -> a
solveRPN expression = head (foldl foldingFunction [] (words expression))
    where foldingFunction stack item = ...

Nós pegamos a expressão e tornamos ela numa lista de itens. Então nós atravessamos a lista de itens com a função de folding. Pense em um [], que representa o acumulador inicial. O acumulador é a nossa pilha, então [] representa uma pilha vazia, que é a que nós começamos. Após pegar a pilha final com um único item, nós chamamos head em nossa lista para pegar este item e então nós aplicamos read.

Então tudo o que nos resta agora é implementar uma função de folding que pega uma pilha, como [4,10], e um item, como "3" e retorna uma nova pilha [3,4,10]. Se a pilha é [4,10] e o item "*", então ela irá retornar [40]. Mas antes disso, vamos passar nossa função para o estilo de ponto livre porque ela tem muitos parênteses que estão me assustando.

import Data.List

solveRPN :: (Num a) => String -> a
solveRPN = head . foldl foldingFunction [] . words
    where   foldingFunction stack item = ...

Ah, Vamos lá. Bem melhor. Então, a função de folding irá pegar uma pilha e um item e retornar uma nova pilha. Nós iremos usar casamento de padrões para pegar os principais itens da pilha e para reconhecer os padrões de operadores como "*" e "-".

solveRPN :: (Num a, Read a) => String -> a
solveRPN = head . foldl foldingFunction [] . words
    where   foldingFunction (x:y:ys) "*" = (x * y):ys
            foldingFunction (x:y:ys) "+" = (x + y):ys
            foldingFunction (x:y:ys) "-" = (y - x):ys
            foldingFunction xs numberString = read numberString:xs

Nós colocamos isso com quatro padrões. Os padrões serão testados do primeiro para o último. Primeiro a função de folding irá ver se o item atual é "*". Se ele é, então ele irá pegar uma lista como [3,4,9,3] e chamará seus primeiros dois elementos x e y respectivamente. Então neste caso, x pode ser 3 e y pode ser 4. ys pode ser [9,3]. Isto irá retornar uma lista que é como ys, apenas se há x e y multiplicado como sua cabeça. Portanto com isso nós iremos retirar os dois números mais ao topo da pilha, multiplica-los e então colocar o resultado de volta na pilha. Se o item não é "*", o casamento de padrão irá falhar e "+" será checado, e assim por diante.

Se o item não é nenhum dos operadores, então nós assumimos que ele é uma string que representa um número. Se ele é um número, nós apenas chamamos read nessa string pra pegar o número dela e retornamos a pilha anterior, mas agora com este número colocado no topo dela.

E é isso! Também notamos que nós adicionamos uma classe extra de restrição a Read a para a declaração da função, porque nós chamamos read em nossa string para pegar um número. Então esta declaração significa que o resultado pode ser apenas do tipo que é parte das classes Num e Read (como Int, Float, etc.).

Para a lista de itens ["2","3","+"], nossa função irá começar atravessando a partir da esquerda. A pilha inicial será []. Ela irá chamar a função de folding com [] como uma pilha (acumulador) e "2" como o item. Como este item não é um operador, ele será lido com read e adicionado ao início de []. Então a nova pilha agora será [2] e a função de folding será chamada com [2] como pilha e ["3"] como um item, produzindo uma nova pilha [3,2]. Então, ela é chamada pela terceira vez com [3,2] como a pilha e "+" como o item. Isto porque estes dois números precisam ser retirados da pilha, somados e então o resultado posto de volta. A pilha final é [5], que é o número que nós retornamos.

Vamos brincar com a nossa função:

ghci> solveRPN "10 4 3 + 2 * -"
-4
ghci> solveRPN "2 3 +"
5
ghci> solveRPN "90 34 12 33 55 66 + * - +"
-3947
ghci> solveRPN "90 34 12 33 55 66 + * - + -"
4037
ghci> solveRPN "90 34 12 33 55 66 + * - + -"
4037
ghci> solveRPN "90 3 -"
87

Legal, ela funciona! Uma coisa boa sobre nossa função é que ela pode ser facilmente modificada para suportar vários outro operadores. Eles sempre tem de ser operadores binários. Por exemplo, nós podemos criar um operador "log" que apenas retira um número da pilha e coloca de volta o seu logaritmo. Nós podemos criar operadores ternários que retiram três números da pilha e colocam o resultado de volta ou operações como "sum" que retiram todos os números e coloca de volta a sua soma.

Vamos modificar nossa função para pegar mais algumas operações. Por causa da simplicidade, nós iremos alterar a declaração do seu tipo para retornar um número do tipo Float.

import Data.List

solveRPN :: String -> Float
solveRPN = head . foldl foldingFunction [] . words
    where   foldingFunction (x:y:ys) "*" = (x * y):ys
            foldingFunction (x:y:ys) "+" = (x + y):ys
            foldingFunction (x:y:ys) "-" = (y - x):ys
            foldingFunction (x:y:ys) "/" = (y / x):ys
            foldingFunction (x:y:ys) "^" = (y ** x):ys
            foldingFunction (x:xs) "ln" = log x:xs
            foldingFunction xs "sum" = [sum xs]
            foldingFunction xs numberString = read numberString:xs

Wow, maravilhoso! / é certamente divisão e ** é a exponenciação de ponto flutuante. Com o operador de logaritmo, nós apenas casamos o padrão com um único elemento e o resto da pilha porquê apenas precisamos de um elemento para calcular um logaritmo natural. Com o operador sum, apenas retornamos a pilha que tínhamos com um elemento que é a soma de todos os elementos que estavam presentes na pilha.

ghci> solveRPN "2.7 ln"
0.9932518
ghci> solveRPN "10 10 10 10 sum 4 /"
10.0
ghci> solveRPN "10 10 10 10 10 sum 4 /"
12.5
ghci> solveRPN "10 2 ^"
100.0

Note que nós podemos incluir números de ponto flutuante em nossas expressões porque read sabe o como ler eles.

ghci> solveRPN "43.2425 0.5 ^"
6.575903

Eu penso que criar uma função que pode calcular arbitrariamente expressões NPI de ponto flutuante e que tem a opção de ser facilmente estendida em 10 linhas é algo muito impressionante.

Uma coisa para notar sobre a nossa função é que ela não é realmente tolerante a falhas. Quando dada uma entrada que não faz sentido, ela irá apenas quebrar tudo. Nós vamos criar uma versão tolerante a falhas com esta declaração de tipo solveRPN :: String -> Maybe Float quando nós aprendermos monads (elas não são assustadoras, confie em mim!). Nós podemos fazer uma coisa agora, mas ela pode ser um pouco tediosa porque pode envolver uma serie de checagens para Nothing em cada passo. Se você está se sentindo preparado para o desafio, você pode seguir em frente e tentar! Dica: você pode usar reads para ver se a leitura foi feita com sucesso ou não.

De Heathrow para Londres

Nosso próximo problema é esse: o avião onde você estava acabou de aterrissar na Inglaterra e você aluga um carro. Você tem uma reunião logo logo e tem que ir do Heathrow até Londres o mais rápido que puder (mas seguramente!).

Há duas estradas principais indo de Heathrow para Londres e há um número de estradas regionais cruzando-as. Leva-se uma quantidade de tempo fixa para se viajar de um cruzamento para outro. Depende de você encontrar o caminho ideal a se tomar para que você chegue a Londres o mais rápido possível! Você começa do lado esquerdo e pode tanto cruzar para a outra estrada principal ou seguir em frente.

Como você pode ver nesta figura, o caminho mais curto de Heathrow para Londres nesse caso é começar pela estrada principal B, cruzar, seguir em frente em A, cruzar novamente e então ir em frente duas vezes em B. Se tomarmos esse caminho, levaremos 75 minutos. Se tivéssemos escolhido qualquer outro caminho, levaria mais tempo que isso.

Nosso trabalho é fazer um programa que recebe uma entrada que representa o sistema de entradas e dá como saída qual é o caminho mais curto atravessando-o. Aqui está como a entrada se pareceria nesse caso:

Para se entender o arquivo de entrada, leia-o de três em três e divida mentalmente o sistema de estradas em seções. Cada seção é composta de uma estrada A, uma estrada B e uma estrada cruzando-as. Para que a entrada elegantemente divida-se em grupos de três, dizemos que há uma última seção de cruzamento que demora 0 minutos para ser atravessada. Isso é porque não nos importamos em que parte de Londres nós chegamos, contanto que estejamos em Londres.

Assim como fizemos quando resolvemos o problema da calculadora RPN, vamos resolver esse problema em três passos:

Esqueça Haskell por um minuto e pense em como nós resolveríamos esse problema na mão.
Pense sobre como vamos representar nossos dados em Haskell.
Descubra como operar sobre esses dados em Haskell para que produzamos a solução.

Na seção da calculadora RPN, primeiro nós descobrimos que quando estávamos calculando uma expressão na mão, tínhamos de manter uma pilha em nossas mentes e então passar um item de cada vez pela expressão. Nós decidimos usar uma lista de strings para representar nossa expressão. Finalmente, usamos uma dobra à esquerda para andar sobre a lista de strings enquanto mantivemos uma pilha para produzir uma solução.

Certo, então como nós poderíamos encontrar o caminho mais curto de Heathrow para Londres na mão? Bem, podemos meramente meio que olhar para a figura inteira e tentar adivinhar qual é o caminho mais curto e esperançosamente daremos um palpite que estará correto. Essa solução funciona para entradas muito pequenas, mas e se nós tivermos uma estrada que tenha 10.000 seções? Caramba! Nós também não poderemos dizer se a nossa solução é a ideal, podemos apenas meio que dizer que estamos bem certos disso.

Essa então não é uma solução boa. Aqui está uma figura simplificada do nosso sistema de estradas:

Pronto, você consegue descobrir qual é o caminho mais curto para o primeiro cruzamento (o primeiro ponto azul em A, marcado A1) na estrada A? É bem trivial. Nós simplesmente vemos se é mais curto seguir diretamente em A ou se é mais curto ir diretamente em B e então cruzar. Óbviamente, é mais barato seguir em frente via B e então cruzar porque isso leva 40 minutos, enquanto que ir direto por A leva 50 minutos. E quanto ao cruzamento B1? A mesma coisa. Vemos que é muito mais barato simplesmente ir diretamente via B (sujeitando-se ao custo de 10 minutos), porque ir por A e então cruzar levaria completos 80 minutos!

Agora sabemos qual é o caminho mais curto para A1 (ir via B e então cruzar, então diremos que isso é B, C com o custo de 40) e sabemos qual é o caminho mais curto para B1 (vá diretamente via B, então é apenas B, custando 10). No fim das contas, esse conhecimento nos ajuda de alguma forma se quisermos saber qual o caminho mais barato para o próximo cruzamento em ambas estradas principais? Caramba, com certeza sim!

Vamos ver qual seria o caminho mais curto para A2. Para chegar em A2, nós vamos ou diretamente de A1 para A2 ou nós vamos em frente de B1 e então cruzamos (lembre-se, podemos apenas ou seguir em frente ou cruzar para o outro lado). E porque conhecemos o custo para A1 e B1, podemos facilmente descobrir qual é o melhor caminho para A2. Custa 40 para chegar em A1 e então 5 para ir de A1 para A2, então isso é B, C, A por um preço de 45. Custa apenas 10 para se chegar em B1, mas então ter-se-ia de gastar adicionais 110 minutos para ir até B2 e então cruzar para o outro lado! Então obviamente, o caminho mais barato para B2 é B, C, A. Do mesmo jeito, o caminho mais barato para B é seguir em frente de A1 e então cruzar para o outro lado.

Talvez você esteja se perguntando: mas e quanto a chegar até A2 por primeiro cruzar em B1 e então seguir adiante? Bem, já cobrimos de B1 até A1 quando estávamos procurando pelo melhor caminho até A1, daí não temos que levar isso em conta no próximo passo.

Agora que temos o melhor caminho para A2 e B2, podemos repetir isso infinitamente até chegarmos no fim. Assim que tivermos conseguido os melhores caminhos para A4 e B4, o que for mais barato é o caminho ótimo!

Então em essência, para a segunda seção, apenas repetimos o passo que fizemos na primeira, só que levamos em conta quais foram os melhores caminhos anteriores em A e B. Poderíamos dizer que também levamos em consideração os melhores caminhos em A e B no primeiro passo, só que eles eram ambos caminhos vazios com um custo de 0.

Aqui está um resumo. Para se conseguir o melhor caminho de Heathrow para Londres, fazemos isso primeiro: vemos qual é o melhor caminho para o próximo cruzamento na estrada principal A. As duas opções são seguir diretamente em frente ou começar na estrada oposta, seguir em frente e então cruzar. Lembramos o custo e o caminho. Usamos o mesmo método para ver qual o melhor caminho para o próximo cruzamento na estrada principal B e não esquecemos disso. Daí, vemos se o caminho para o próximo cruzamento na estrada principal A é mais barato se formos a partir do cruzamento anterior em A ou se formos a partir do cruzamento anterior em B e então cruzar. Lembramos do caminho mais barato e então fazemos o mesmo para o cruzamento oposto a esse. Fazemos isso para seção até chegarmos no fim. Uma vez que tenhamos chegado no fim, o mais barato dos dois caminhos que nós tivermos é nosso caminho ideal.

Então em essência, nós mantemos um caminho mais curto na estrada A e um caminho mais curto na estrada B e quando chegamos no fim, o mais curto desses dois é nosso caminho. Nós agora sabemos como encontrar o caminho mais curto na mão. Se você tivesse tempo o suficiente, papel e lápis, você poderia encontrar o caminho mais curto através de um sistema de estradas com qualquer número de seções.

Próximo passo! Como representamos esse sistema de estradas com os tipos de dados de Haskell? Uma forma é pensar nos pontos iniciais e cruzamentos como nodos de um grafo que apontam pra outros cruzamentos. Se imaginarmos que os pontos iniciais na verdade apontam de um pro outro com uma estrada quem tenha o tamanho 1, vemos que todo cruzamento (ou nodo) aponta para o nodo do outro lado e também para o próximo no seu lado. Exceto pelos últimos nodos, eles apenas apontam para o outro lado.

data Node = Node Road Road | EndNode Road
data Road = Road Int Node

Um nodo é tanto um nodo normal, que tem informação sobre a estrada que leva para a outra estrada principal e sobre a estrada que leva para o próximo nodo, ou é um nodo final, que só tem informação sobre a estrada para a outra estrada principal. Uma estrada mantém informação sobre quão longa ela é e para qual nodo ela aponta. Por exemplo, a primeira parte da estrada na estrada principal A seria Road 50 a1 onde a1 seria um nodo Node x y, onde x e y são estradas que apontam para B1 e A1.

Outra forma seria usar Maybe para as partes da estrada que apontam adiante. Cada nodo tem uma parte que aponta para para a estrada oposta, mas apenas aqueles nodos que não são os finais têm partes de estradas que apontam adiante.

data Node = Node Road (Maybe Road)
data Road = Road Int Node

Essa é uma forma aceitável para se representar um sistema de estradas em Haskell e poderíamos certamente resolver esse problema com ela, mas talvez nós pudéssemos pensar em algo mais simples? Se pensarmos voltando para nossa solução feita à mão, nós sempre apenas checamos os tamanhos de três partes de estrada por vez: a parte da estrada na estrada A, sua parte oposta na estrada B e a parte C, que toca nessas duas partes e as conecta. Quando estávamos procurando pelo menor caminho até A1 e B1, tínhamos apenas que lidar com os tamanhos das três primeiras partes, as quais tinham os tamanhos de 50, 10 e 30. Vamos chamar isso de uma seção. Então o sistema de estradas que usamos para esse exemplo pode ser facilmente representado como quatro seções: 50, 10, 30, 5, 90, 20, 40, 2, 25, e 10, 8, 0.

É sempre bom manter nossos tipos de dados o mais simples possível, apesar de não ser tão simples!

data Section = Section { getA :: Int, getB :: Int, getC :: Int } deriving (Show)
type RoadSystem = [Section]

Isso é bem perfeito! É simples assim e eu sinto que isso funcionará perfeitamente na implementação de nossa solução. Section é um tipo algébrico simples que contem três inteiros para os tamanhos das três partes das estradas. Nós também introduzimos um tipo sinônimo, dizendo que RoasSystem é uma lista de seções.

Também poderíamos usar uma tripla de (Int, Int, Int) para representar uma seção de estrada. Usar tuplas em vez de nossos próprios tipos é bom para algumas pequenas coisas localizadas, mas é geralmente melhor fazer um novo tipo para coisas desse tipo. Isso dá ao sistema de tipos mais informação sobre o que é o quê. Podemos usar (Int, Int, Int) para representar uma seção de estrada ou um vetor em um espaço 3D e podemos operar nesses dois, mas isso nos permite misturar as coisas. Se usarmos os tipos de dados Section e Vector, então não podemos acidentalmente adicionar um vetor com uma secção de um sistema de estradas.

Nosso sistema de estradas de Heathrow para Londres agora pode ser representado dessa forma:

heathrowToLondon :: RoadSystem
heathrowToLondon = [Section 50 10 30, Section 5 90 20, Section 40 2 25, Section 10 8 0]

Tudo que precisamos agora é implementar em Haskell a solução que inventamos anteriormente. Qual deveria ser a declaração de tipo para uma função que calcula o caminho mais curto para um dado sistema de estradas qualquer? Ela tem que receber o sistema de entradas como parâmetro e retornar um caminho. Vamos representar um caminho também como uma lista. Vamos introduzir um tipo Label que é apenas uma enumeração tanto de A, B ou C. Vamos também criar um tipo sinônimo: Path.

data Label = A | B | C deriving (Show)
type Path = [(Label, Int)]

Nossa função, nós a chamaremos de optimalPath, deveria então ter uma declaração de tipo de optimalPath :: RoadSystem -> Path. Se chamada com o sistema de estradas heathrowToLondon, deveria retornar o seguinte caminho:

[(B,10),(C,30),(A,5),(C,20),(B,2),(B,8)]

Vamos ter que passar pela lista das seções da esquerda para a direita e manter o caminho ideal em A e o caminho ideal em B durante a passagem. Vamos acumular o melhor caminho a medida que passamos pela lista, da esquerda para a direita. O que isso parece? Ding, ding, ding! Exatamente, UMA DOBRA PARA A ESQUERDA!

Quando estávamos fazendo a solução na mão, havia um passo que nós repetimos várias e várias vezes. Envolvia checar os novos caminhos ideias em A e B. Por exemplo, no começo os caminhos ótimos eram [] e [] para A e B respectivamente. Examinamos a seção Section 50 10 30 e concluímos que o novo caminho ideal para A1 era [(B, 10), (C, 30)] e o caminho ideal para B1 era [(B, 10)]. Se você olhar para esse passo como uma função, ela leva um par de caminhos e uma seção e produz um novo par de caminhos. O tipo é (Path, Path) -> Section -> (Path, Path). Vamos em frente implementar essa função, porque ela está destinada a ser útl.

Dica: vai ser útil porque (Path, Path) -> Section -> (Path, Path) pode ser usada como a função binária de uma dobra à esquerda, que tem que ser do tipo a -> b -> a

roadStep :: (Path, Path) -> Section -> (Path, Path)
roadStep (pathA, pathB) (Section a b c) = 
    let priceA = sum $ map snd pathA
        priceB = sum $ map snd pathB
        forwardPriceToA = priceA + a
        crossPriceToA = priceB + b + c
        forwardPriceToB = priceB + b
        crossPriceToB = priceA + a + c
        newPathToA = if forwardPriceToA <= crossPriceToA
                        then (A,a):pathA
                        else (C,c):(B,b):pathB
        newPathToB = if forwardPriceToB <= crossPriceToB
                        then (B,b):pathB
                        else (C,c):(A,a):pathA
    in  (newPathToA, newPathToB)

O que está acontecendo aqui? Primeiro, calcular o preço ideal na estrada A baseado no melhor até agora em A e fazemos o mesmo para B. Fazemos sum $ map snd pathA, então se pathA for algo do tipo [(A,100),(C,20)], priceA torna-se 120. forwardPriceToA é o preço que pagaríamos se fossemos para o próximo cruzamento em A se fossemos pra lá diretamente do cruzamento anterior em A. Isso iguala o melhor preço do nosso A anterior, mais o tamanho da parte de A da seção atual. crossPriceToA é o preço que pagaríamos se nós fossemos para o próximo A indo em frente do B anterior e então cruzando. É o melhor preço para o B anterior até agora mais o tamanho de B da seção mais o tamanho de C da seção. Determinamos forwardPriceToB e crossPriceToB da mesma maneira.

Agora que sabemos qual é o melhor caminho para A e para B, precisamos apenas criar os novos caminhos para A e B baseados nisso. Se for mais barato ir para A apenas por seguir em frente, setamos newPathToA para ser (A,a):pathA. Basicamente nós prefixamos a Label A e o tamanho da seção a para o caminho ideal em A até agora. Basicamente, dizemos que o melhor caminho para o próximo cruzamento A é o caminho para o cruzamento A anterior e então uma seção adiante via A. Lembre-se, A é apenas um rótulo, enquanto que a tem o tipo de Int. Por que nós prefixamos em vez de fazer pathA ++ [(A,a)]? Bem, adicionar um elemento no início de uma lista (também conhecido como “consing”) é muito mais rápido que adicioná-lo no fim. Isso significa que o caminho estará invertido para o lado errado quando dobrarmos sobre uma lista com essa função, mas é fácil inverter a lista depois. Se for mais fácil chegar no próximo cruzamento A indo direto pela estrada B e então cruzando, então newPathToA é o antigo caminho para B a partir do qual segue-se em frente e cruza para A. Fazemos a mesma coisa para newPathToB, só que tudo agora está espelhado.

Finalmente, retornamos newPathToA e newPathToB em um par.

Vamos rodar essa função na primeira seção de heathrowToLondon. Porque é a primeira seção, os melhores caminhos nos parâmetros A e B será uma par de listas vazias.

ghci> roadStep ([], []) (head heathrowToLondon)
([(C,30),(B,10)],[(B,10)])

Lembre-se, os caminhos estão invertidos, então leia-os da direita para a esquerda. Disso, podemos ler que o melhor caminho para o próximo A é começar de B e então cruzar para A e que o melhor caminho para o próximo B é apenas ir diretamente adiante do ponto inicial em B.

Dica de otimização: quando fazemos priceA = sum $ map snd pathA, estamos calculando o preço do caminho em todo passo. Não teríamos de fazer isso se implementássemos roadStep como uma função de (Path, Path, Int, Int) -> Section -> (Path, Path, Int, Int) onde os inteiros representam o melhor preço em A e em B.

Agora que temos uma função que leva um par de caminhos e uma seção e produz um novo caminho ideal, podemos apenas facilmente fazer uma dobra a esquerda sobre uma lista de seções. roadStep é chamada com ([],[]) e a primeira seção retorna um par de caminhos ideias para tal seção. Então, é chamada com esse par de caminhos e com a próxima seção e assim por diante. Quando tivermos passado por todas as seções, teremos um par com os caminhos ideais e o mais curto deles será a resposta. Com isso em mente, podemos implementar optimalPath.

optimalPath :: RoadSystem -> Path
optimalPath roadSystem =
    let (bestAPath, bestBPath) = foldl roadStep ([],[]) roadSystem
    in  if sum (map snd bestAPath) <= sum (map snd bestBPath)
            then reverse bestAPath
            else reverse bestBPath

Nós dobramos pela esquerda sobre roadSystem (lembre-se, é uma lista de seções) com o acumulador inicial sendo um par de caminhos vazios. O resultado dessa dobra é um par de caminhos, então casamos padrões no par para conseguir os caminhos em si. Então, checamos qual desses é mais barato e retornamos ele. Antes de retorná-lo, tambem o invertemos, porque os caminhos ótimos até agora estavam invertidos devido a nossa escolha de prefixá-los em vez de anexá-los no final.

Vamos testar isso!

ghci> optimalPath heathrowToLondon
[(B,10),(C,30),(A,5),(C,20),(B,2),(B,8),(C,0)]

Esse é o resultado que deveríamos conseguir! Incrível! Ele difere um pouco do noso resultado esperado porque há um passo (C,0) no fim, que significa que nós cruzamos para a outra estrada assim que estamos em Londres, mas como esse cruzamento não custa nada, ainda é o resultado correto.

Temos a função que encontra um caminho ótimo, agora apenas temos que ler a representação textual do sistema de estradas da entrada padrão, convertê-la no tipo RoadSystem, rodar isso pela nossa função optimalPath e imprimir o caminho.

Primeiramente, vamos fazer uma função que recebe uma lista e a divide em grupos do mesmo tamanho. Vamos chamá-la groupsOf. Para o parâmetro de [1..10], groupsOf 3 deve retornar [[1,2,3],[4,5,6],[7,8,9],[10]].

groupsOf :: Int -> [a] -> [[a]]
groupsOf 0 _ = undefined
groupsOf _ [] = []
groupsOf n xs = take n xs : groupsOf n (drop n xs)

Uma função recursiva padrão. Por um xs de [1..10] e um n de 3, isso é igual a [1,2,3] : groupsOf 3 [4,5,6,7,8,9,10]. Quando a recursão estiver feita, temos nossa lista em grupos de três. Aqui está nossa função main, que lê da entrada padrão, cria um RoadSystem a partir disso e imprime o caminho mais curto:

import Data.List

main = do
    contents <- getContents
    let threes = groupsOf 3 (map read $ lines contents)
        roadSystem = map (\[a,b,c] -> Section a b c) threes
        path = optimalPath roadSystem
        pathString = concat $ map (show . fst) path
        pathPrice = sum $ map snd path
    putStrLn $ "The best path to take is: " ++ pathString
    putStrLn $ "The price is: " ++ show pathPrice

Primeiro, pegamos todo o conteúdo da entrada padrão. Então, chamamos lines como nosso conteúdo para converter algo como "50\n10\n30\n... para ["50","10","30".. e então nós mapeamos read para converter isso em uma lista de números. Chamamos groupsOf 3 nela para que nós a tornemos uma lista de listas de tamanho 3. Mapeamos o lambda (\[a,b,c] -> Section a b c) sobre essa lista de listas. Como você pode ver, lambda apenas pega uma lista de tamanho 3 e transforma-a numa seção. Então roadSystem é agora nosso sistema de estradas e tem até o tipo correto, a saber RoadSystem (ou [Section]). Chamamos optimalPath com isso e então conseguimos o caminho e o preço em uma representação textual legal e a imprimimos.

Salvamos o texto a seguir

em um arquivo chamado paths.txt e então o alimentamos para nosso programa.

$ cat paths.txt | runhaskell heathrow.hs
The best path to take is: BCACBBC
The price is: 75

Funciona como mágica! Você pode usar seu conhecimento do módulo Data.Random para gerar um sistema de estradas muito maior, o qual você pode então usar para alimentar o que acabamos de escrever. Se você obtiver estouros de pilha, tente usar foldl' em vez de foldl, porque foldl' é estrito.